题目内容
11.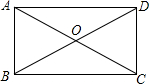 如图,在矩形ABCD中,对角线AC与BD相交于点O,AC=8,∠BOC=120°,则矩形的面积是( )
如图,在矩形ABCD中,对角线AC与BD相交于点O,AC=8,∠BOC=120°,则矩形的面积是( )| A. | 16 | B. | 32 | C. | 8$\sqrt{3}$ | D. | 16$\sqrt{3}$ |
分析 根据OB=OC,∠ABC=90°,以及∠BOC=120°,可得出∠OBC=∠OCB=30°,进而得到AB=$\frac{1}{2}$AC=4;根据勾股定理即可求出BC,进而得出矩形ABCD的面积.
解答 解:∵四边形ABCD是矩形,
∴OB=OC,∠ABC=90°,
又∵∠BOC=120°,
∴∠OBC=∠OCB=30°,
∴AB=$\frac{1}{2}$AC=$\frac{1}{2}$×8=4;
∵AB2+BC2=AC2,
∴BC=$\sqrt{A{C}^{2}-A{B}^{2}}$=4$\sqrt{3}$,
∴矩形ABCD的面积=AB×BC=4×4 $\sqrt{3}$=16 $\sqrt{3}$.
故选D.
点评 本题主要考查了矩形的性质以及勾股定理的运用,解题时注意:在直角三角形中,30°角所对的直角边等于斜边的一半.

练习册系列答案
 精英口算卡系列答案
精英口算卡系列答案 应用题点拨系列答案
应用题点拨系列答案
相关题目
2.下列事件中,是必然事件的是( )
| A. | 上海明天下雨 | |
| B. | 从一副新扑克牌中任意抽取10张牌,其中有5张A | |
| C. | 10只小白兔关在3个笼子里,至少有一个笼子关的小白兔超过3只 | |
| D. | 小明走到路口时,交通信号灯正好是绿灯 |
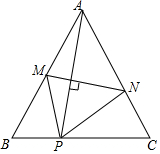 如图,P为等边△ABC中BC边上一点,AP的垂直平分线交AB,AC于M、N.
如图,P为等边△ABC中BC边上一点,AP的垂直平分线交AB,AC于M、N.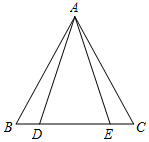 阅读并填空:如图,已知在△ABC中,AB=AC,点D、E在边BC上,且AD=AE.试说明BD=CE的理由.
阅读并填空:如图,已知在△ABC中,AB=AC,点D、E在边BC上,且AD=AE.试说明BD=CE的理由.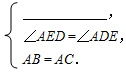
 若把如图所示网格设计成一个投镖靶子,使得随意投掷一次飞镖击中红色区域的概率为$\frac{3}{8}$,那么需要在网格中涂成红色的小正方形的个数为6.
若把如图所示网格设计成一个投镖靶子,使得随意投掷一次飞镖击中红色区域的概率为$\frac{3}{8}$,那么需要在网格中涂成红色的小正方形的个数为6.