题目内容
19.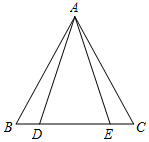 阅读并填空:如图,已知在△ABC中,AB=AC,点D、E在边BC上,且AD=AE.试说明BD=CE的理由.
阅读并填空:如图,已知在△ABC中,AB=AC,点D、E在边BC上,且AD=AE.试说明BD=CE的理由.解:因为AB=AC,
所以∠B=∠C(等边对等角).
因为AD=AE,
所以∠AED=∠ADE(等边对等角).
在△ABE和△ACD中,
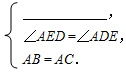
所以△ABE≌△ACD(AAS).
所以BE=CD(全等三角形的对应边相等).
所以BE-DE=CD-DE(等式性质).
所以BD=CE(等式性质).
分析 有AB=AC,AD=AE,根据等腰三角形的性质得∠B=∠C,∠ADE=∠AED,再根据全等三角形的判定方法易证△ABE≌△ACD,根据全等的性质得BE=CD,利用等式的性质有BE-DE=CD-DE,即有BD=CE.
解答 解:∵AB=AC,
∴∠B=∠C,
∵AD=AE,
∴∠ADE=∠AED,
在△ABE与△ACD中,
∵$\left\{\begin{array}{l}{∠B=∠C}\\{∠AEB=∠ADC}\\{AB=AC}\end{array}\right.$,
∴△ABE≌△ACD(AAS),
∴BE=CD,
∴BE-DE=CD-DE,
即BD=CE.
故答案为:∠B=∠C;AD=AE;AAS;BE=CD;BE-DE=CD-DE.
点评 本题考查了全等三角形的判定与性质:有两组角分别相等,且其中一组角所对的边对应相等,那么这两个三角形全等;全等三角形的对应边相等.也考查了等腰三角形的性质.

练习册系列答案
相关题目
7.与数轴上的点具有一一对应关系的是( )
| A. | 全体有理数 | B. | 全体无理数 | C. | 全体实数 | D. | 正实数和负实数 |
11.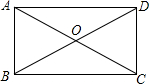 如图,在矩形ABCD中,对角线AC与BD相交于点O,AC=8,∠BOC=120°,则矩形的面积是( )
如图,在矩形ABCD中,对角线AC与BD相交于点O,AC=8,∠BOC=120°,则矩形的面积是( )
 如图,在矩形ABCD中,对角线AC与BD相交于点O,AC=8,∠BOC=120°,则矩形的面积是( )
如图,在矩形ABCD中,对角线AC与BD相交于点O,AC=8,∠BOC=120°,则矩形的面积是( )| A. | 16 | B. | 32 | C. | 8$\sqrt{3}$ | D. | 16$\sqrt{3}$ |
9.在平面直角坐标系中,如果点P(a,b)到y轴的距离为2,那么( )
| A. | a=2 | B. | a=±2 | C. | b=2 | D. | b=±2 |
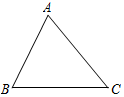 如图,把△ABC绕点C顺时针旋转40°后,得到△A′B′C,其中点A、B分别与点A′、B′对应,且点B′落在边AB上,A′B′与边AC相交于点D,如果∠A′DC=90°,那么∠A=50度.
如图,把△ABC绕点C顺时针旋转40°后,得到△A′B′C,其中点A、B分别与点A′、B′对应,且点B′落在边AB上,A′B′与边AC相交于点D,如果∠A′DC=90°,那么∠A=50度.