题目内容
20.若|m|,|n|是直角三角形的两条直角边,则这个直角三角形的斜边长为$\frac{5}{3}$,其中m,n满足$\sqrt{-{m}^{2}+2m+3}$+|2m-4|+(3n-4m)2=4-2m.分析 直接利用算术平方根以及绝对值、偶次方的性质得出m,n的值,进而得出答案.
解答 解:∵$\sqrt{-{m}^{2}+2m+3}$+|2m-4|+(3n-4m)2=4-2m,
而等号左边三个算式都是非负数,
∴$\sqrt{-{m}^{2}+2m+3}$=0,(3n-4m)2=0,
4-2m≥0,
∴-m2+2m+3=-(m-1)2+4=0,
解得:m=-1或3,
当m=-1时,3n-4m=0,
解得:n=-$\frac{4}{3}$,
同时满足4-2m≥0,
所以直角三角形的斜边长为:$\sqrt{(-1)^{2}+(-\frac{4}{3})^{2}}$=$\frac{5}{3}$;
②当m=3时,3n-4m=0,解得:n=4,
但此时4-2m=-2<0,与题意不符,舍去,
所以直角三角形的斜边长为$\frac{5}{3}$.
故答案为:$\frac{5}{3}$.
点评 此题主要考查了勾股定理以及算术平方根以及绝对值、偶次方的性质,正确得出m,n的值是解题关键.

练习册系列答案
 轻松暑假总复习系列答案
轻松暑假总复习系列答案
相关题目
8.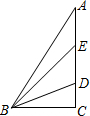 如图,在△ABC中∠C=90°,D、E为AC上的两点,且AE=DE,BD平分∠EBC,则下列说法不正确的是( )
如图,在△ABC中∠C=90°,D、E为AC上的两点,且AE=DE,BD平分∠EBC,则下列说法不正确的是( )
 如图,在△ABC中∠C=90°,D、E为AC上的两点,且AE=DE,BD平分∠EBC,则下列说法不正确的是( )
如图,在△ABC中∠C=90°,D、E为AC上的两点,且AE=DE,BD平分∠EBC,则下列说法不正确的是( )| A. | BE是△ABD的中线 | B. | BD是△BCE的角平分线 | ||
| C. | ∠ABE=∠EBD=∠DBC | D. | BC是△ABE的高 |
5.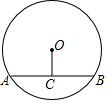 排水管的截面如图,水面宽AB=8,圆心O到水面的距离OC=3,则排水管的半径等于( )
排水管的截面如图,水面宽AB=8,圆心O到水面的距离OC=3,则排水管的半径等于( )
 排水管的截面如图,水面宽AB=8,圆心O到水面的距离OC=3,则排水管的半径等于( )
排水管的截面如图,水面宽AB=8,圆心O到水面的距离OC=3,则排水管的半径等于( )| A. | 5 | B. | 6 | C. | 8 | D. | 4 |
 在△ABC中,AB=AC
在△ABC中,AB=AC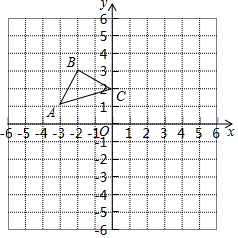 如图,在平面直角坐标系中,A(-3,1),B(-2,3),C(0,2),画出△ABC关于x轴对称的△A′B′C′,再画出△A′B′C′关于y轴对称的△A″B″C″,那么△A″B″C″与△ABC有什么位置关系,请说明理由.
如图,在平面直角坐标系中,A(-3,1),B(-2,3),C(0,2),画出△ABC关于x轴对称的△A′B′C′,再画出△A′B′C′关于y轴对称的△A″B″C″,那么△A″B″C″与△ABC有什么位置关系,请说明理由.