题目内容
4.已知(2-a)(3-a)=5.(1)求(a-2)2+(3-a)2的值;
(2)求a2+a-2的值;
(3)求$\frac{3{a}^{2}+3}{{a}^{4}-4{a}^{3}+4}$的值.
分析 (1)根据(a-2)2+(3-a)2=[(a-2)+(3-a)]2-2(a-2)(3-a),结合已知条件代入即可解决问题.
(2)根据条件先求出a+a-1=5,再利用完全平方公式计算即可.
(3)分子分母利用a2=5a-1,进行降幂,即可解决问题.
解答 解:(1)∵(2-a)(3-a)=5,
∴(a-2)2+(3-a)2=[(a-2)+(3-a)]2-2(a-2)(3-a)
=1-2×5
=-9;
(2)∵(2-a)(3-a)=5,
∴6-2a-3a+a2=5,
∴a2-5a=-1,
∴a+a-1=5,
∴(a+a-1)2=25,
∴a2+2+a-2=25,
∴a2+a-2=23.
(3)∵a2=5a-1,
∴原式=$\frac{3(5a-1)+3}{(5a-1)^{2}-4a(5a-1)+4}$=$\frac{15a}{25{a}^{2}-10a+1-20{a}^{2}+4a+4}$=$\frac{15a}{5{a}^{2}-6a+5}$=$\frac{15a}{5(5a-1)-6a+5}$=$\frac{15a}{19a}$=$\frac{15}{19}$.
点评 本题考查整式的混合运算、乘法公式等知识,解题的关键是灵活运用公式,学会把多项式降幂处理,属于中考常考题型.

练习册系列答案
相关题目
12.已知A(x1,y1)是一次函数y=-x+b+1图象上一点,若x1<0,y1<0,则b的取值范围是( )
| A. | b<0 | B. | b>0 | C. | b>-1 | D. | b<-1 |
16.若3×9m×27m=311,则m的值为( )
| A. | 5 | B. | 4 | C. | 3 | D. | 2 |
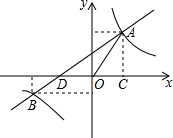 如图,在平面直角坐标系中,双曲线y=$\frac{m}{x}$与直线y=kx+b相交于A、B两点,过点A作AC⊥x轴于点C,其中AC=4,tan∠AOC=$\frac{4}{3}$且点B的坐标为(-6,n).
如图,在平面直角坐标系中,双曲线y=$\frac{m}{x}$与直线y=kx+b相交于A、B两点,过点A作AC⊥x轴于点C,其中AC=4,tan∠AOC=$\frac{4}{3}$且点B的坐标为(-6,n).