Question

19．如图，在边长为（2m+3）的正方形纸片中剪出一个边长为（m+3）的正方形之后，剩余部分可剪拼成一个长方形，若拼成的长方形一边长为m，求另一边长．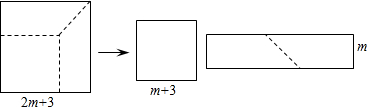

Answer 1

分析 由于边长为（2m+3）的正方形纸片剪出一个边长为m的正方形之后，剩余部分又剪拼成一个矩形（不重叠无缝隙），那么根据正方形的面积剩余部分的面积可以求出，而矩形一边长为m，利用矩形的面积公式即可求出另一边长．

解答 解：依题意得剩余部分为：（2m+3）²-（m+3）²=4m²+12m+9-m²-6m-9=3m²+6m，
而拼成的矩形一边长为m，
∴另一边长是（3m²+6m）÷m=3m+6．
答：若拼成的长方形一边长为m，则另一边长为：3m+6．

点评 本题考查了因式分解的应用，解决本题的关键是熟记平方差、完全平分公式．