题目内容
17. 某工厂接到一批粽子生产任务,按要求在15天内完成,约定这批粽子的出厂价为每只6元,为按时完成任务,该工厂招收了新工人,设新工人王浩第x天生产的粽子数量为y只,y与x满足如下关系:
某工厂接到一批粽子生产任务,按要求在15天内完成,约定这批粽子的出厂价为每只6元,为按时完成任务,该工厂招收了新工人,设新工人王浩第x天生产的粽子数量为y只,y与x满足如下关系:y=$\left\{\begin{array}{l}{54x,(0≤x≤5)}\\{30x+120,(5≤x≤15)}\end{array}\right.$,
(1)王浩第几天生产的粽子数量为360只?
(2)如图,设第x天每只粽子的成本是p元,p与x之间的关系可用图中的函数图形来刻画.若王浩第x天创造的利润为w元,求w关于x的函数表达式,并求出第几天的利润最大,最大利润是多少元?(利润=出厂价-成本)
分析 (1)把y=360代入y=30x+120,解方程即可求得;
(2)根据图象求得成本p与x之间的关系,然后根据利润等于出厂价减去成本价,然后整理即可得到W与x的关系式,再根据一次函数的增减性和二次函数的增减性解答.
解答 解:(1)设王浩第n天生产的粽子数量为360只,
由题意可知:30n+120=360,
解得n=8.
答:第8天生产的粽子数量为420只.
(2)由图象得,当0≤x≤9时,p=4.1;
当9≤x≤15时,设P=kx+b,
把点(9,4.1),(15,4.7)代入得,
$\left\{\begin{array}{l}{9k+b=4.1}\\{15k+b=4.7}\end{array}\right.$,解得$\left\{\begin{array}{l}{k=0.1}\\{b=3.2}\end{array}\right.$,
∴p=0.1x+3.2,
①0≤x≤5时,w=(6-4.1)×54x=102.6x,当x=5时,w最大=513(元);
②5<x≤9时,w=(6-4.1)×(30x+120)=57x+228,
∵x是整数,
∴当x=9时,w最大=741(元);
③9<x≤15时,w=(6-0.1x-3.2)×(30x+120)=-3x2+72x+336,
∵a=-3<0,
∴当x=-$\frac{b}{2a}$=12时,w最大=768(元);
综上,当x=12时,w有最大值,最大值为768.
答:第12天的利润最大,最大利润是768元
点评 本题考查的是二次函数在实际生活中的应用,主要是利用二次函数的增减性求最值问题,利用一次函数的增减性求最值,难点在于读懂题目信息,列出相关的函数关系式.

练习册系列答案
相关题目
12.已知点P是线段MN的黄金分割点,MP>NP,且MP=($\sqrt{5}$-1)cm,则NP等于( )
| A. | 2cm | B. | (3-$\sqrt{5}$)cm | C. | ($\sqrt{5}$-1)cm | D. | ($\sqrt{5}$+1)cm |
2. 如图放置一个水管三叉接头,则其俯视图是( )
如图放置一个水管三叉接头,则其俯视图是( )
 如图放置一个水管三叉接头,则其俯视图是( )
如图放置一个水管三叉接头,则其俯视图是( )| A. |  | B. |  | C. |  | D. |  |
9. 如图所示,将矩形ABCD绕点A顺时针旋转到矩形AB′C′D′的位置,旋转角为α(0°<α<90°),若∠1=115°,则α=( )
如图所示,将矩形ABCD绕点A顺时针旋转到矩形AB′C′D′的位置,旋转角为α(0°<α<90°),若∠1=115°,则α=( )
 如图所示,将矩形ABCD绕点A顺时针旋转到矩形AB′C′D′的位置,旋转角为α(0°<α<90°),若∠1=115°,则α=( )
如图所示,将矩形ABCD绕点A顺时针旋转到矩形AB′C′D′的位置,旋转角为α(0°<α<90°),若∠1=115°,则α=( )| A. | 20° | B. | 25° | C. | 30° | D. | 35° |
 某中学了解本校学生对球类运动的爱好情况,分为足球、篮球、排球、其他四个方面调查若干名学生,每人只选其中之一,统计后绘制成不完整的“折线统计图”(扇形统计图),根据信息解答下列问题:
某中学了解本校学生对球类运动的爱好情况,分为足球、篮球、排球、其他四个方面调查若干名学生,每人只选其中之一,统计后绘制成不完整的“折线统计图”(扇形统计图),根据信息解答下列问题: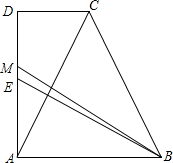 如图,直角梯形ABCD中,E为AD边上的中点,过A作AC⊥BE,交CD边于C,M是AD边上一点,且有BM=DM+AD,AD=BA.
如图,直角梯形ABCD中,E为AD边上的中点,过A作AC⊥BE,交CD边于C,M是AD边上一点,且有BM=DM+AD,AD=BA.