题目内容
已知Rt△ABC的两条直角边之比为3:4,△ABC∽△A1B1C1,若△A1B1C1的最短边长12cm,则△A1B1C1最长边的中线长为 cm.
考点:相似三角形的性质
专题:
分析:由Rt△ABC的两条直角边之比为3:4,△ABC∽△A1B1C1,可得△A1B1C1的两条直角边之比也为3:4,又△A1B1C1的最短边长12cm,则其两条直角边分别为12cm,16cm,再根据勾股定理求出斜边,然后利用直角三角形斜边上的中线等于斜边的一半即可求解.
解答:
解:∵Rt△ABC的两条直角边之比为3:4,△ABC∽△A1B1C1,
∴△A1B1C1的两条直角边之比也为3:4,
又∵△A1B1C1的最短边长12cm,
∴其两条直角边分别为12cm,16cm,
∴斜边=
=20cm,
∴△A1B1C1最长边的中线长为
×20=10cm.
故答案为10.
∴△A1B1C1的两条直角边之比也为3:4,
又∵△A1B1C1的最短边长12cm,
∴其两条直角边分别为12cm,16cm,
∴斜边=
| 122+162 |
∴△A1B1C1最长边的中线长为
| 1 |
| 2 |
故答案为10.
点评:本题考查了相似三角形对应边的比相等的性质,勾股定理以及直角三角形的性质,得出△A1B1C1的两条直角边分别为12cm,16cm是解题的关键.

练习册系列答案
 学期复习一本通学习总动员期末加暑假延边人民出版社系列答案
学期复习一本通学习总动员期末加暑假延边人民出版社系列答案 芒果教辅暑假天地重庆出版社系列答案
芒果教辅暑假天地重庆出版社系列答案
相关题目
 教练对小明推铅球的录像进行技术分析,发现铅球行进高度y(m)与水平距离x(m)之间的关系为y=-
教练对小明推铅球的录像进行技术分析,发现铅球行进高度y(m)与水平距离x(m)之间的关系为y=-| 1 |
| 12 |
| 2 |
| 3 |
| 5 |
| 3 |
| A、10m | B、3m |
| C、4m | D、2m或10m |
在直角坐标系中,一直线l向下平移3个单位后所得直线b经过点A(0,3),将直线b绕点A顺时针旋转60°后所得直线经过点B(-
,0),则直线l的函数关系式为( )
| 3 |
A、y=-
| ||||
B、y=-
| ||||
C、y=-
| ||||
D、y=-
|
 如图,以△ABC的BC边上一点O为圆心的圆,经过A、B两点,且与BC边交于点E,D为BE的下半圆弧的中点,连接AD交BC于F,且AC=FC.求证:AC是⊙O的切线.
如图,以△ABC的BC边上一点O为圆心的圆,经过A、B两点,且与BC边交于点E,D为BE的下半圆弧的中点,连接AD交BC于F,且AC=FC.求证:AC是⊙O的切线.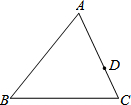 如图,在△ABC中,∠C>∠B,AB=12,AC=9,D是AC上一点,AD=6,在AB上取一点E,使以A,D,E三点为顶点的三角形与△ABC相似,则AE的长为
如图,在△ABC中,∠C>∠B,AB=12,AC=9,D是AC上一点,AD=6,在AB上取一点E,使以A,D,E三点为顶点的三角形与△ABC相似,则AE的长为

 如图,四边形ABCD,∠ABC与∠DCE的平分线交于P.
如图,四边形ABCD,∠ABC与∠DCE的平分线交于P.