题目内容
18．
如图，在Rt△ABC中，∠C=90°，BD平分∠ABC，DE垂直平分AB，CD=1，则AD=2．
分析 根据角平分线的性质，可得DE的长，根据直角三角形的性质，可得AD．
解答 解：由在Rt△ABC中，∠C=90°，BD平分∠ABC，DE垂直平分AB，得
∠CAD=∠ABD=∠A，DE=CD=1，
则∠A=30°．
由30°的直角边等斜边的一半，得
AD=2DE=2
故答案为：2．
点评 本题考查了含30°角的直角三角形，利用角平分线的性质得出DE的长是解题关键，同时利用了直角三角形的性质．
练习册系列答案
每课必练系列答案
巧学巧练系列答案
相关题目
如图，AB、CD相交于点O，OE是∠AOC的平分线，∠BOD=70°，∠EOF=65°，则∠AOF的度数为30°．
6．下列乘法中，不能运用平方差公式进行运算的是（ ）
| A． | （x+a）（x-a） | B． | （-x-b）（x-b） | C． | （a+b）（-a-b） | D． | （b+m）（m-b） |
13．一个长方形花坛长是x3米，宽是（xy2）2米，则此长方形花坛的面积为（ ）
| A． | x6y4米2 | B． | x6y2米2 | C． | x5y4米2 | D． | x5y2米2 |
10．若反比例函数y=$\frac{3-m}{x}$，当x＞0时，函数值y随x的增大而减小，则（ ）
| A． | m＜0 | B． | m＞0 | C． | m＜3 | D． | m＞3 |
7．
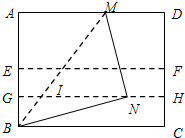如图，对折矩形纸片ABCD，使BC与AD重合，折痕为EF，把纸片展平；再一次折叠纸片，使BC与EF重合，折痕为GH，把纸片展平；再一次折叠纸片，使点A落在GH上的点N处，并使折痕经过点B，折痕BM交GH于点I．若AB=4cm，则GI的长为（ ）
如图，对折矩形纸片ABCD，使BC与AD重合，折痕为EF，把纸片展平；再一次折叠纸片，使BC与EF重合，折痕为GH，把纸片展平；再一次折叠纸片，使点A落在GH上的点N处，并使折痕经过点B，折痕BM交GH于点I．若AB=4cm，则GI的长为（ ）| A． | $\frac{\sqrt{10}}{4}$cm | B． | $\frac{3}{4}$cm | C． | $\frac{4}{5}$cm | D． | $\frac{\sqrt{15}}{5}$cm |