题目内容
13.设x与y2成反比例,y与z2成正比例,当x=24时,y=2,当y=18时,z=3,求当z=1时,x的值是多少?分析 设x=$\frac{k}{{y}^{2}}$,y=k′z2,将x=24,y=2;y=18,z=3分别代入;求出k与k′的值,再把z=1代入,即可求出x的值.
解答 解:设x=$\frac{k}{{y}^{2}}$,y=k′z2,
将x=24,y=2;y=18,z=3分别代入,
得24=$\frac{k}{{2}^{2}}$,18=k′×32,
解得k=96,k′=2,
所以x=$\frac{96}{{y}^{2}}$,y=2z2,
当z=1时,y=2,x=24.
点评 本题考查了用待定系数法求反比例函数、正比例函数的解析式,掌握待定系数法的应用关键是点的坐标,即把点坐标代入得到关于系数的方程,求解即可.

练习册系列答案
 鸿图图书寒假作业假期作业吉林大学出版社系列答案
鸿图图书寒假作业假期作业吉林大学出版社系列答案
相关题目
5.某风景的团体购买门票票价如下:
今甲、乙两个旅行团,已知甲团人数小于50人,乙团人数不超过100人,若分别购票,两团共计应付门票费1950元,若合在一起作为一个团体共计应门票1545元.
(1)请你判断乙团的人数是否也少于50人;
(2)求甲、乙两旅行团各有多少人;
(3)甲旅行团单独购票,有无更省钱的方案?说明理由.
| 购票人数 | 1~50 | 51~100 | 100人以上 |
| 每人门票 | 20元 | 18元 | 15元 |
(1)请你判断乙团的人数是否也少于50人;
(2)求甲、乙两旅行团各有多少人;
(3)甲旅行团单独购票,有无更省钱的方案?说明理由.
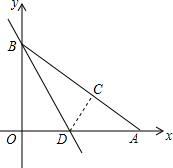 如图,在平面直角坐标系中,点A、B的坐标分别为(8,0)、(0,6),将△OAB折叠,使OB边落在AB边上,点O与点C重合,折痕为BD.
如图,在平面直角坐标系中,点A、B的坐标分别为(8,0)、(0,6),将△OAB折叠,使OB边落在AB边上,点O与点C重合,折痕为BD. 如图,在Rt△ABC中,∠C=90°,BD平分∠ABC,DE垂直平分AB,CD=1,则AD=2.
如图,在Rt△ABC中,∠C=90°,BD平分∠ABC,DE垂直平分AB,CD=1,则AD=2.