题目内容
20. 下列图形都是由同样大小的棋子按一定的规律组成,其中第①个图形有1颗棋子,第②个图形一共有6颗棋子,第③个图形一共有16颗棋子,…,则第⑧个图形中棋子的颗数为( )
下列图形都是由同样大小的棋子按一定的规律组成,其中第①个图形有1颗棋子,第②个图形一共有6颗棋子,第③个图形一共有16颗棋子,…,则第⑧个图形中棋子的颗数为( )| A. | 226 | B. | 181 | C. | 141 | D. | 106 |
分析 设第n个图形中棋子的颗数为an(n为正整数),根据部分an的变化可找出变化规律“an=$\frac{5}{2}$n2-$\frac{5}{2}$n+1”,代入n=8即可得出结论.
解答 解:设第n个图形中棋子的颗数为an(n为正整数),
观察,发现规律:a1=1,a2=1+3+2=6,a3=1+3+5+4+3=16,…,
∴an=1+3+5+…+(2n-1)+(2n-2)+…+n=n2+$\frac{(n-1)(3n-2)}{2}$=$\frac{5}{2}$n2-$\frac{5}{2}$n+1,
当n=8时,a8=$\frac{5}{2}$×82-$\frac{5}{2}$×8+1=141.
故选C.
点评 本题考查了规律型中图形的变化类,根据图形中棋子数目的变化找出变化规律是解题的关键.

练习册系列答案
相关题目
10.$\root{3}{(-1)^{2}}$的立方根是( )
| A. | 1 | B. | -1 | C. | 10 | D. | -10 |
11.世界上最小的开花结果植物是澳大利亚的出水浮萍,这种植物的果实像一个微小的无花果,质量只有0.000000076克,用科学记数法表示是( )
| A. | 0.76×10-9克 | B. | 7.6×10-8克 | C. | 7.6×108克 | D. | 7.6×10-9克 |
15.-$\frac{1}{3}$的倒数是( )
| A. | $\frac{1}{3}$ | B. | -$\frac{1}{3}$ | C. | -3 | D. | 3 |
5.在代数式$\frac{1}{2}$x-y,5a,x2-y+$\frac{2}{3}$,$\frac{1}{π}$,xyz,-$\frac{5}{y}$,$\frac{x+y+z}{3}$中,有( )
| A. | 5个整式 | |
| B. | 4个单项式,3个多项式 | |
| C. | 6个整式,4个单项式 | |
| D. | 6个整式,单项式与多项式的个数相同 |
12.若一组数据1,5,7,x 的极差10,则x的值为( )
| A. | 11或-3 | B. | 17或-3 | C. | 11 | D. | -3 |
9.某厂今年一月的总产量为500吨,三月的总产量为720吨,平均每月增长率是x,列方程 ( )
| A. | 500(1+2x)=720 | B. | 720(1+x)2=500 | C. | 500(1+x2)=720 | D. | 500(1+x)2=720 |
10.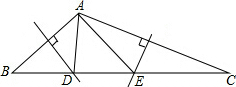 如图,△ABC的两边AB和AC的垂直平分线分别交BC于D、E,若∠BAC=120°,则∠DAE的度数为( )
如图,△ABC的两边AB和AC的垂直平分线分别交BC于D、E,若∠BAC=120°,则∠DAE的度数为( )
 如图,△ABC的两边AB和AC的垂直平分线分别交BC于D、E,若∠BAC=120°,则∠DAE的度数为( )
如图,△ABC的两边AB和AC的垂直平分线分别交BC于D、E,若∠BAC=120°,则∠DAE的度数为( )| A. | 20° | B. | 30° | C. | 45° | D. | 60° |