题目内容
5.在代数式$\frac{1}{2}$x-y,5a,x2-y+$\frac{2}{3}$,$\frac{1}{π}$,xyz,-$\frac{5}{y}$,$\frac{x+y+z}{3}$中,有( )| A. | 5个整式 | |
| B. | 4个单项式,3个多项式 | |
| C. | 6个整式,4个单项式 | |
| D. | 6个整式,单项式与多项式的个数相同 |
分析 根据整式、单项式、多项式的概念即可判断.
解答 解:$\frac{1}{2}$x-y,5a,x2-y+$\frac{2}{3}$,$\frac{1}{π}$,xyz,$\frac{x+y+z}{3}$是整式,
其中式$\frac{1}{2}$x-y,x2-y+$\frac{2}{3}$,$\frac{x+y+z}{3}$是多项式,
5a,$\frac{1}{π}$,xyz是单项式,
故选(D)
点评 本题考查整式的概念与分类,属于基础题型.

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
16.当x=1时,下列分式的值为0的是( )
| A. | $\frac{x-1}{{{x^2}-1}}$ | B. | $\frac{x+1}{{{x^2}-1}}$ | C. | $\frac{1-x}{{{x^2}-1}}$ | D. | $\frac{{{x^2}-1}}{x+1}$ |
13.已知⊙O的半径为3,圆心O到直线L的距离为2,则直线L与⊙O的位置关系是( )
| A. | 不能确定 | B. | 相离 | C. | 相切 | D. | 相交 |
20. 下列图形都是由同样大小的棋子按一定的规律组成,其中第①个图形有1颗棋子,第②个图形一共有6颗棋子,第③个图形一共有16颗棋子,…,则第⑧个图形中棋子的颗数为( )
下列图形都是由同样大小的棋子按一定的规律组成,其中第①个图形有1颗棋子,第②个图形一共有6颗棋子,第③个图形一共有16颗棋子,…,则第⑧个图形中棋子的颗数为( )
 下列图形都是由同样大小的棋子按一定的规律组成,其中第①个图形有1颗棋子,第②个图形一共有6颗棋子,第③个图形一共有16颗棋子,…,则第⑧个图形中棋子的颗数为( )
下列图形都是由同样大小的棋子按一定的规律组成,其中第①个图形有1颗棋子,第②个图形一共有6颗棋子,第③个图形一共有16颗棋子,…,则第⑧个图形中棋子的颗数为( )| A. | 226 | B. | 181 | C. | 141 | D. | 106 |
10.对于函数y=-x2+2x-2,使得y随x的增大而增大的x的取值范围是( )
| A. | x>1 | B. | x≥0 | C. | x≤0 | D. | x<1 |
14.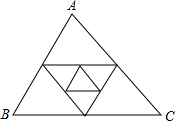 如图,已知△ABC的周长为1,连结△ABC三边的中点构成第二个三角形,再连结第二个三角形三边的中点构成第三个三角形,依此类推,则第2016个三角形的周长为( )
如图,已知△ABC的周长为1,连结△ABC三边的中点构成第二个三角形,再连结第二个三角形三边的中点构成第三个三角形,依此类推,则第2016个三角形的周长为( )
 如图,已知△ABC的周长为1,连结△ABC三边的中点构成第二个三角形,再连结第二个三角形三边的中点构成第三个三角形,依此类推,则第2016个三角形的周长为( )
如图,已知△ABC的周长为1,连结△ABC三边的中点构成第二个三角形,再连结第二个三角形三边的中点构成第三个三角形,依此类推,则第2016个三角形的周长为( )| A. | $\frac{1}{2015}$ | B. | $\frac{1}{2016}$ | C. | $\frac{1}{{2}^{2015}}$ | D. | $\frac{1}{{2}^{2016}}$ |
15.从一副54张的扑克牌中任意抽一张,以下事件中可能性最大的是( )
| A. | 抽到方块8 | B. | 抽到K牌 | C. | 抽到梅花 | D. | 抽到大王 |
 如图,抛物线y=ax2-4x+c经过坐标原点O,且与x轴交于点A(-4,0)
如图,抛物线y=ax2-4x+c经过坐标原点O,且与x轴交于点A(-4,0)