题目内容
5. 如图,两个边长分别为a,b(a>b)的正方形连在一起,三点C,B,F在同一直线上,反比例函数y=$\frac{k}{x}$在第一象限的图象经过小正方形右下顶点E.若OB2-BE2=10,则k的值是( )
如图,两个边长分别为a,b(a>b)的正方形连在一起,三点C,B,F在同一直线上,反比例函数y=$\frac{k}{x}$在第一象限的图象经过小正方形右下顶点E.若OB2-BE2=10,则k的值是( )| A. | 3 | B. | 4 | C. | 5 | D. | 4$\sqrt{5}$ |
分析 设E点坐标为(a,b),则AO+DE=a,AB-BD=b,根据△ABO和△BED都是等腰直角三角形,得到EB=$\sqrt{2}$BD,OB=$\sqrt{2}$AB,再根据OB2-EB2=10,运用平方差公式即可得到(AO+DE)(AB-BD)=5,进而得到a•b=5,据此可得k=5.
解答  解:设E点坐标为(a,b),则AO+DE=a,AB-BD=b,
解:设E点坐标为(a,b),则AO+DE=a,AB-BD=b,
∵△ABO和△BED都是等腰直角三角形,
∴EB=$\sqrt{2}$BD,OB=$\sqrt{2}$AB,BD=DE,OA=AB,
∵OB2-EB2=10,
∴2AB2-2BD2=10,
即AB2-BD2=5,
∴(AB+BD)(AB-BD)=5,
∴(AO+DE)(AB-BD)=5,
∴a•b=5,
∴k=5.
故选:C.
点评 本题考查了反比例函数图象上点的坐标特征,反比例函数y=$\frac{k}{x}$(k为常数,k≠0)的图象是双曲线,图象上的点(x,y)的横纵坐标的积是定值k,即xy=k.解题时注意数形结合思想的运用.

练习册系列答案
相关题目
15.已知x=1是方程x2+mx+n=0的一个根,则代数式m2+2mn+n2的值为( )
| A. | -1 | B. | 1 | C. | -2 | D. | 2 |
13. 如图,点A,B,C,D在数轴上,其中表示互为相反数的点是( )
如图,点A,B,C,D在数轴上,其中表示互为相反数的点是( )
 如图,点A,B,C,D在数轴上,其中表示互为相反数的点是( )
如图,点A,B,C,D在数轴上,其中表示互为相反数的点是( )| A. | 点A与点D | B. | 点B与点D | C. | 点A与点C | D. | 点B与点C |
15. 如图是几何体的三视图,该几何体是( )
如图是几何体的三视图,该几何体是( )
 如图是几何体的三视图,该几何体是( )
如图是几何体的三视图,该几何体是( )| A. | 圆锥 | B. | 圆柱 | C. | 正三棱锥 | D. | 正三棱柱 |
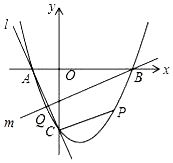 抛物线y=x2+bx+c与x轴交于A、B两点,B点坐标为(3,0),与y轴交于点C(0,-3)
抛物线y=x2+bx+c与x轴交于A、B两点,B点坐标为(3,0),与y轴交于点C(0,-3)