题目内容
10.已知x=2是关于x的方程x2-(m+4)x+4m=0的一个实数根,并且这个方程的两个实数根恰好是等腰三角形ABC的两条边长,则△ABC的周长为( )| A. | 6 | B. | 8 | C. | 10 | D. | 8或10 |
分析 先利用一元二次方程解的定义把x=2代入方程x2-(m+4)x+4m=0得m=2,则方程化为x2-6x+8=0,然后解方程后利用三角形三边的关系确定三角形的三边,最后就是三角形的周长.
解答 解:把x=2代入方程x2-(m+4)x+4m=0得4-2(m+4)+4m=0,解得m=2,
方程化为x2-6x+8=0,解得x1=4,x2=2,
因为2+2=4,
所以三角形三边为4、4、2,
所以△ABC的周长为10.
故选C.
点评 本题考查了一元二次方程的解:能使一元二次方程左右两边相等的未知数的值是一元二次方程的解.也考查了三角形三边的关系.

练习册系列答案
 步步高达标卷系列答案
步步高达标卷系列答案
相关题目
20.十一点十分这一时刻,分针和时针的夹角是( )
| A. | 70° | B. | 75° | C. | 80° | D. | 85° |
5. 如图,两个边长分别为a,b(a>b)的正方形连在一起,三点C,B,F在同一直线上,反比例函数y=$\frac{k}{x}$在第一象限的图象经过小正方形右下顶点E.若OB2-BE2=10,则k的值是( )
如图,两个边长分别为a,b(a>b)的正方形连在一起,三点C,B,F在同一直线上,反比例函数y=$\frac{k}{x}$在第一象限的图象经过小正方形右下顶点E.若OB2-BE2=10,则k的值是( )
 如图,两个边长分别为a,b(a>b)的正方形连在一起,三点C,B,F在同一直线上,反比例函数y=$\frac{k}{x}$在第一象限的图象经过小正方形右下顶点E.若OB2-BE2=10,则k的值是( )
如图,两个边长分别为a,b(a>b)的正方形连在一起,三点C,B,F在同一直线上,反比例函数y=$\frac{k}{x}$在第一象限的图象经过小正方形右下顶点E.若OB2-BE2=10,则k的值是( )| A. | 3 | B. | 4 | C. | 5 | D. | 4$\sqrt{5}$ |
15.不等式组 $\left\{{\begin{array}{l}{\frac{x+1}{2}<1}\\{2x-1≤3x}\end{array}}\right.$的整数解的个数是( )
| A. | 1 | B. | 2 | C. | 3 | D. | 4 |
2.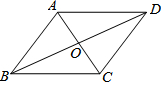 如图,平行四边形ABCD的对角线AC与BD相交于点O,要使它成为矩形,需再添加的条件是( )
如图,平行四边形ABCD的对角线AC与BD相交于点O,要使它成为矩形,需再添加的条件是( )
 如图,平行四边形ABCD的对角线AC与BD相交于点O,要使它成为矩形,需再添加的条件是( )
如图,平行四边形ABCD的对角线AC与BD相交于点O,要使它成为矩形,需再添加的条件是( )| A. | AO=OC | B. | AC=BD | C. | AC⊥BD | D. | BD平分∠ABC |
20.关于x的一元二次方程mx2+2x+1=0有两个不相等的实数根,则m的取值范围是( )
| A. | m<1 | B. | m≤1 | C. | m<1且m≠0 | D. | m≤1且m≠0 |
 如图,平面直角坐标系中,直线y=x+2与x轴交于点A,与y轴交于点D,B为AO的中点,DC⊥DB交x轴于点C,E在y轴上,且OC=OE,经过B、E、C三点的抛物线与直线AD交于F、G两点,与其对称轴交于M点
如图,平面直角坐标系中,直线y=x+2与x轴交于点A,与y轴交于点D,B为AO的中点,DC⊥DB交x轴于点C,E在y轴上,且OC=OE,经过B、E、C三点的抛物线与直线AD交于F、G两点,与其对称轴交于M点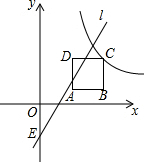 边长为a的正方形ABCD在平面直角坐标系中的位置如图所示,其中AB与x轴平行(点B在点A的右侧),点A的坐标为(2,1),反比例函数y=$\frac{m}{x}$经过点C,直线l:y=kx-2(k≠0)与y轴交于点E.
边长为a的正方形ABCD在平面直角坐标系中的位置如图所示,其中AB与x轴平行(点B在点A的右侧),点A的坐标为(2,1),反比例函数y=$\frac{m}{x}$经过点C,直线l:y=kx-2(k≠0)与y轴交于点E.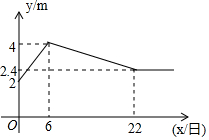 如图,是皖韵水库进入5月份以来的水位y米与x日的函数图象,为了避免过度捕捞,当水位低于3米时就不适宜渔船打捞作业,根据图象可知,5月份能打捞的天数有( )天.
如图,是皖韵水库进入5月份以来的水位y米与x日的函数图象,为了避免过度捕捞,当水位低于3米时就不适宜渔船打捞作业,根据图象可知,5月份能打捞的天数有( )天.