题目内容
已知,如图,O为正方形对角线的交点,BE平分∠DBC,交DC于点E,延长BC到点F,使CF=CE,连结DF,交BE的延长线于点G,连结OG.
(1)求证:△BCE≌△DCF.
(2)判断OG与BF有什么关系,证明你的结论.
(3)若DF2=8﹣4
 ,求正方形ABCD的面积?
,求正方形ABCD的面积?


【考点】正方形的性质;全等三角形的判定与性质;勾股定理.
【分析】(1)利用正方形的性质,由全等三角形的判定定理SAS即可证得△BCE≌△DCF;
(2)首先证明△BDG≌△BGF,从而得到OG是△DBF的中位线,即可得出答案;
(3)设BC=x,则DC=x,BD=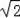
 x,由△BGD≌△BGF,得出BF=BD,CF=(
x,由△BGD≌△BGF,得出BF=BD,CF=(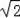
 ﹣1)x,利用勾股定理DF2=DC2+CF2,解得x2=2,即正方形ABCD的面积是2.
﹣1)x,利用勾股定理DF2=DC2+CF2,解得x2=2,即正方形ABCD的面积是2.
【解答】解:(1)证明:在△BCE和△DCF中,
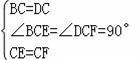
 ,
,
∴△BCE≌△DCF(SAS);
(2)OG∥BF且OG=
 BF,
BF,
理由:如图,


∵BE平分∠DBC,
∴∠2=∠3,
在△BGD和△BGF中,
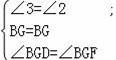
 ,
,
∴△BGD≌△BGF(ASA),
∴DG=GF,
∵O为正方形ABCD的中心,
∴DO=OB,
∴OG是△DBF的中位线,
∴OG∥BF且OG=
 BF;
BF;
(3)设BC=x,则DC=x,BD=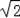
 x,由(2)知△BGD≌△BGF,
x,由(2)知△BGD≌△BGF,
∴BF=BD,
∴CF=(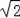
 ﹣1)x,
﹣1)x,
∵DF2=DC2+CF2,
∴x2+[(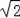
 ﹣1)x]2=8﹣4
﹣1)x]2=8﹣4
 ,解得x2=2,
,解得x2=2,
∴正方形ABCD的面积是2.

练习册系列答案
 轻松暑假总复习系列答案
轻松暑假总复习系列答案
相关题目
 的解集是
的解集是 ,则(
,则(  )
) B、
B、 C、
C、 D、
D、
 有意义,则x的取值范围是(
有意义,则x的取值范围是(  )
)
 ]=3,求满足条件的所有正整数x.
]=3,求满足条件的所有正整数x.