题目内容
7.计算:2$\sqrt{12}$×$\frac{\sqrt{3}}{4}$÷5$\sqrt{2}$-($\sqrt{\frac{1}{8}}$+$\sqrt{18}$)分析 直接利用二次根式的乘除运算法则化简二次根式进而求出即可.
解答 解:原式=4$\sqrt{3}$×$\frac{\sqrt{3}}{4}$×$\frac{1}{5\sqrt{2}}$-$\frac{\sqrt{2}}{4}$-3$\sqrt{2}$
=$\frac{3\sqrt{2}}{10}$-$\frac{\sqrt{2}}{4}$-3$\sqrt{2}$
=$\frac{6\sqrt{2}}{20}$-$\frac{5\sqrt{2}}{20}$-$\frac{60\sqrt{2}}{20}$
=-$\frac{59}{20}$$\sqrt{2}$.
点评 此题主要考查了二次根式的混合运算,正确化简二次根式是解题关键.

练习册系列答案
相关题目
15.已知二元一次方程3x-y=1,当x=2时,y-8等于( )
| A. | 5 | B. | -3 | C. | -7 | D. | 7 |
2.下列计算正确的是( )
| A. | $\sqrt{4}$+$\sqrt{5}$=$\sqrt{9}$ | B. | $\sqrt{(-2)^{2}}$=-2 | C. | $\sqrt{18}$÷3=$\sqrt{6}$ | D. | 3$\sqrt{2}$-$\sqrt{2}$=2$\sqrt{2}$ |
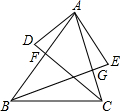 已知,△ABC中,BE⊥AC于G,CD⊥AB于F,BA=BE,CA=CD,以下结论:①∠D=∠E;②DF=GE;③$\frac{AF}{AG}$=$\frac{AC}{AB}$;④$\frac{DF}{CF}$=$\frac{EG}{BG}$,其中正确的有①③④(填上你认为所有正确结论的序号).
已知,△ABC中,BE⊥AC于G,CD⊥AB于F,BA=BE,CA=CD,以下结论:①∠D=∠E;②DF=GE;③$\frac{AF}{AG}$=$\frac{AC}{AB}$;④$\frac{DF}{CF}$=$\frac{EG}{BG}$,其中正确的有①③④(填上你认为所有正确结论的序号).