题目内容
20.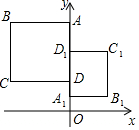 如图,正方形ABCD与正方形A1B1C1D1关于某点中心对称.已知A,D1,D三点的坐标分别是(0,4),(0,3),(0,2).
如图,正方形ABCD与正方形A1B1C1D1关于某点中心对称.已知A,D1,D三点的坐标分别是(0,4),(0,3),(0,2).(1)求对称中心Q的坐标,并仅用直尺画出Q点的位置;
(2)写出顶点B,C,B1,C1的坐标.
分析 (1)根据对称中心的性质,可得对称中心的坐标是D1D的中点,据此解答即可.
(2)首先根据A,D的坐标分别是(0,4),(0,2),求出正方形ABCD与正方形A1B1C1D1的边长是多少,然后根据A,D1,D三点的坐标分别是(0,4),(0,3),(0,2),判断出顶点B,C,B1,C1的坐标各是多少即可.
解答  解:(1)根据对称中心的性质,可得
解:(1)根据对称中心的性质,可得
对称中心的坐标是D1D的中点,
∵D1,D的坐标分别是(0,3),(0,2),
∴对称中心的坐标是(0,2.5),
连接BB1交AA1于Q,
则点Q即为所求;
(2)∵A,D的坐标分别是(0,4),(0,2),
∴正方形ABCD与正方形A1B1C1D1的边长都是:4-2=2,
∴B,C的坐标分别是(-2,4),(-2,2),
∵A1D1=2,D1的坐标是(0,3),
∴A1的坐标是(0,1),
∴B1,C1的坐标分别是(2,1),(2,3),
综上,可得顶点B,C,B1,C1的坐标分别是(-2,4),(-2,2),(2,1),(2,3).
点评 此题主要考查了旋转变换,坐标与图形的性质的应用,根据题意得出旋转后对应点位置是解题关键.

练习册系列答案
相关题目
5.a的相反数是( )
| A. | |a| | B. | $\frac{1}{a}$ | C. | -a | D. | 以上都不对 |
12.关于二次函数y=-2x2+1,下列说法错误的是( )
| A. | 图象开口向下 | B. | 图象的对称轴为x=$\frac{1}{2}$ | ||
| C. | 函数最大值为1 | D. | 当x>1时,y随x的增大而减小 |