题目内容
直线y1=k1x+b1与直线y2=k2x+b2交于(-3,2),且分别过(-
,0)和(1,-2),求这两条直线与y轴所围成的三角形面积.
| 3 |
| 2 |
考点:两条直线相交或平行问题
专题:
分析:把点(-3,2),(-
,0)代入y1=k1x+b1即可求得y1的解析式,把点(-3,2),(1,-2)代入y2=k2x+b2即可求得y2的解析式,求出两直线与y轴的交点,即可求解.
| 3 |
| 2 |
解答:解:把点(-3,2),(-
,0)代入y1=k1x+b1得
,
解得
,
所以y1=-
x-2.
把点(-3,2),(1,-2)代入y2=k2x+b2得
,
解得
,
所以y2=-x-1.
y1、y2与y轴的交点分别是:(0,-2),(0,-1),
y1、y2与y轴所围成的三角形的底长为|-2-(-1)|=1,高为y1与y2交于点的横坐标即3.
故y1、y2与y轴所围成的三角形的面积为
×3×1=
.
| 3 |
| 2 |
|
解得
|
所以y1=-
| 4 |
| 3 |
把点(-3,2),(1,-2)代入y2=k2x+b2得
|
解得
|
所以y2=-x-1.
y1、y2与y轴的交点分别是:(0,-2),(0,-1),
y1、y2与y轴所围成的三角形的底长为|-2-(-1)|=1,高为y1与y2交于点的横坐标即3.
故y1、y2与y轴所围成的三角形的面积为
| 1 |
| 2 |
| 3 |
| 2 |
点评:此题考查两条直线相交的问题,注意利用一次函数的特点,列出方程,求出未知数再求得解析式;求三角形的面积时找出高和底边长即可.

练习册系列答案
 浙大优学小学年级衔接捷径浙江大学出版社系列答案
浙大优学小学年级衔接捷径浙江大学出版社系列答案
相关题目
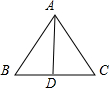 如图,在△ABC中,AD平分∠BAC.求证:
如图,在△ABC中,AD平分∠BAC.求证: