题目内容
13.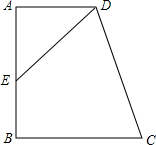 如图,AD∥BC,AB⊥BC,DC平分∠ADC,且E是AB的中点,问,AD,BC与CD之间有何数量关系?请证明你的结论.
如图,AD∥BC,AB⊥BC,DC平分∠ADC,且E是AB的中点,问,AD,BC与CD之间有何数量关系?请证明你的结论.
分析 首先要作辅助线,连接CE,作EF⊥CD,根据角平分线性质求出AE=EF=BE,然后证△FDE≌△ADE及△FCE≌△BCE,推出AD=DF及BC=CF,即可得出答案.
解答 解:AD+BC=CD,
理由是:连接CE,作EF⊥CD,
∵AB⊥BC,AD∥BC,
∴AB⊥AD,
∵DE平分∠ADC,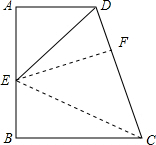
∴EF=ED,
∵E为DC中点,
∴CE=BE,
∴EF=BE,
∵AB⊥BC,
∴∠B=90°=∠CFE,
在Rt△CFE和Rt△CBE中,
$\left\{\begin{array}{l}{BE=EF}\\{CE=CE}\end{array}\right.$,
∴Rt△CFE≌Rt△CBE(HL),
∴BC=CF,
同理可证Rt△ADE≌Rt△FDE(HL),
∴AD=DF
∵DF+CF=CD,
∴AD+BC=CD.
点评 本题考查了角平分线性质以及全等三角形的性质和判定的应用,熟悉角平分线性质是解决问题的关键.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
8.超市9月1日到5日的收入、支出情况如表
运用你学的知识,给商店简单的记一笔帐.
(1)哪几天是亏本,那几天是盈利的?
(2)9月1日到5日,该超市总支出是多少?
| 日期 | 1日 | 2日 | 3日 | 4日 | 5日 |
| 支出(元) | 150 | 260 | 180 | 130 | 210 |
| 收入(元) | 160 | 240 | 150 | 180 | 300 |
(1)哪几天是亏本,那几天是盈利的?
(2)9月1日到5日,该超市总支出是多少?
 如图,△ABC中,中线AD=4,AB=6,求AC的取值范围.
如图,△ABC中,中线AD=4,AB=6,求AC的取值范围. 如图所示,已知数轴上有数a代表的点A和数b代表的点B,点A、点B在数轴原点的两侧,数b的绝对值是数a的绝对值的3倍,且点A与点B之间的距离为8,求a、b的值.
如图所示,已知数轴上有数a代表的点A和数b代表的点B,点A、点B在数轴原点的两侧,数b的绝对值是数a的绝对值的3倍,且点A与点B之间的距离为8,求a、b的值.