题目内容
2.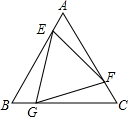 等边△ABC的面积为1,E、F、G是其各条边上的5等分点,其位置如图,那么三角形EFG的面积为$\frac{13}{25}$.
等边△ABC的面积为1,E、F、G是其各条边上的5等分点,其位置如图,那么三角形EFG的面积为$\frac{13}{25}$.
分析 由于△BEG、△CGF、△AEF是全等的,所以只要求出其中一个三角形的面积就可求出△EFG的面积.连接EC,可得△BEC的面积是△ABC面积的五分之四,△BEG的面积是△BEC面积的五分之一.
解答 解:连接EC,如图,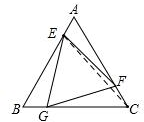
∵E点是AB的五等分点,
∴${S}_{△BCE}=\frac{4}{5}{S}_{△ABC}=\frac{4}{5}$,
∵G点是BC的五等分点,
∴${S}_{△BEG}=\frac{1}{5}{S}_{△BCE}=\frac{4}{25}$,
同理:${S}_{△CGF}={S}_{△AEF}=\frac{4}{25}$,
∴S△GEF=S△ABC-3S△BEG=$\frac{13}{25}$.
故答案为$\frac{13}{25}$.
点评 本题主要考查了等积变换,难度不大,属于基础题.若两个三角形的高相同,则面积之比等于底之比,这是原理是解答本题的关键.

练习册系列答案
 中考利剑中考试卷汇编系列答案
中考利剑中考试卷汇编系列答案 教育世家状元卷系列答案
教育世家状元卷系列答案 黄冈课堂作业本系列答案
黄冈课堂作业本系列答案
相关题目
7.抛物线y=-(x+2)2-5的顶点坐标是( )
| A. | (-2,5) | B. | (2,5) | C. | (-2,-5) | D. | (2,-5) |
14.如果多项式x2+ax+b可因式分解为(x-1)(x+2),则a、b的值为( )
| A. | a=1,b=2 | B. | a=1,b=-2 | C. | a=-1,b=-2 | D. | a=-1,b=2 |
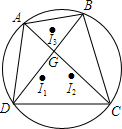 如图,四边形ABCD内接于圆,对角线AC、BD交于点G,I1、I2、I3分别为△ADC、△BDC、△ABG的内心.证明:I3G⊥I1I2.
如图,四边形ABCD内接于圆,对角线AC、BD交于点G,I1、I2、I3分别为△ADC、△BDC、△ABG的内心.证明:I3G⊥I1I2.