题目内容
14.如果多项式x2+ax+b可因式分解为(x-1)(x+2),则a、b的值为( )| A. | a=1,b=2 | B. | a=1,b=-2 | C. | a=-1,b=-2 | D. | a=-1,b=2 |
分析 已知分解结果利用多项式乘以多项式法则计算,再利用多项式相等的条件求出a与b的值即可.
解答 解:根据题意得:x2+ax+b=(x-1)(x+2)=x2+x-2,
则a=1,b=-2,
故选B
点评 此题考查了因式分解-十字相乘法,熟练掌握十字相乘法是解本题的关键.

练习册系列答案
相关题目
5. 如图所示,A、B、C为长方体的三个顶点,则△ABC的形状是( )
如图所示,A、B、C为长方体的三个顶点,则△ABC的形状是( )
 如图所示,A、B、C为长方体的三个顶点,则△ABC的形状是( )
如图所示,A、B、C为长方体的三个顶点,则△ABC的形状是( )| A. | 锐角三角形 | B. | 直角三角形 | C. | 钝角三角形 | D. | 无法确定 |
19.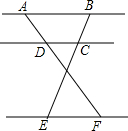 如图所示,已知AB∥CD∥EF,那么下列结论正确的是( )
如图所示,已知AB∥CD∥EF,那么下列结论正确的是( )
 如图所示,已知AB∥CD∥EF,那么下列结论正确的是( )
如图所示,已知AB∥CD∥EF,那么下列结论正确的是( )| A. | $\frac{AD}{DF}$=$\frac{BC}{CE}$ | B. | $\frac{BC}{CE}$=$\frac{DF}{AD}$ | C. | $\frac{CD}{EF}$=$\frac{BC}{BE}$ | D. | $\frac{CD}{EF}$=$\frac{AD}{AF}$ |
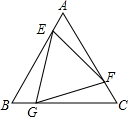 等边△ABC的面积为1,E、F、G是其各条边上的5等分点,其位置如图,那么三角形EFG的面积为$\frac{13}{25}$.
等边△ABC的面积为1,E、F、G是其各条边上的5等分点,其位置如图,那么三角形EFG的面积为$\frac{13}{25}$. 如图,在△ABC中,∠A=90°,D为BC上一点,过D作ED⊥BC交AC于E,若AB=6,AC=8,ED=3,则CD的长为4.
如图,在△ABC中,∠A=90°,D为BC上一点,过D作ED⊥BC交AC于E,若AB=6,AC=8,ED=3,则CD的长为4.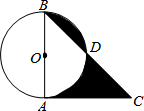 如图,在⊙O中,直径AB=2,CA切⊙O于A,BC交⊙O于D,若∠C=45°,
如图,在⊙O中,直径AB=2,CA切⊙O于A,BC交⊙O于D,若∠C=45°,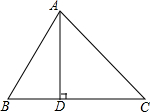 如图,在△ABC中,AD⊥BC于D,tan∠BAD=$\frac{1}{2}$,∠ACD=45°,AB=5,求AC的长.
如图,在△ABC中,AD⊥BC于D,tan∠BAD=$\frac{1}{2}$,∠ACD=45°,AB=5,求AC的长.