题目内容
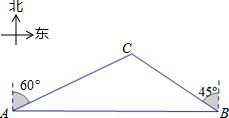 如图,一天,我国一渔政船航行到A处时,发现正东方向的我领海区域B处有一可疑渔船,可疑渔船正向西北方向航行,我渔政船立即沿北偏东60°方向航行,在我领海区域的C处截获可疑渔船.我渔政船的航行路程AC为18是海里,问可疑渔船的航行路程BC是多少海里?(结果保留根号)
如图,一天,我国一渔政船航行到A处时,发现正东方向的我领海区域B处有一可疑渔船,可疑渔船正向西北方向航行,我渔政船立即沿北偏东60°方向航行,在我领海区域的C处截获可疑渔船.我渔政船的航行路程AC为18是海里,问可疑渔船的航行路程BC是多少海里?(结果保留根号)考点:解直角三角形的应用-方向角问题
专题:
分析:过点C作CD⊥AB交AB于点D.在Rt△ABD中,求出AC,在Rt△CBD中,求出CD,从而求出AB的长.
解答: 解:如图,过点C作CD⊥AB交AB于点D.
解:如图,过点C作CD⊥AB交AB于点D.
∵在Rt△ABD中,AC=18海里,∠CAD=30°,
∴CD=AC•sin30°=18×
=9(海里),
∴在Rt△CBD中,CD=9,∠CBD=45°,
BC=CD+sin45°=9+
=9
(海里).
答:我渔政船的航行路程是9
海里.
 解:如图,过点C作CD⊥AB交AB于点D.
解:如图,过点C作CD⊥AB交AB于点D.∵在Rt△ABD中,AC=18海里,∠CAD=30°,
∴CD=AC•sin30°=18×
| 1 |
| 2 |
∴在Rt△CBD中,CD=9,∠CBD=45°,
BC=CD+sin45°=9+
| ||
| 2 |
| 2 |
答:我渔政船的航行路程是9
| 2 |
点评:本题考查了解直角三角形的应用--方向角问题,结合航海中的实际问题,将解直角三角形的相关知识有机结合,体现了数学应用于实际生活的思想.

练习册系列答案
相关题目
化简
×
的结果是( )
| 5 |
|
A、
| ||||
B、
| ||||
C、
| ||||
D、
|
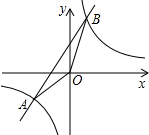 如图,已知A(-2,-2)、B(n,4)是一次函数y=kx+b的图象和反比例函数y=
如图,已知A(-2,-2)、B(n,4)是一次函数y=kx+b的图象和反比例函数y=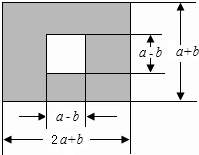 如图,某地有块长为(2a+b)米,宽为(a+b)米的长方形地块,规划部门计划将阴影部分进行绿化,中间将搞一雕塑.
如图,某地有块长为(2a+b)米,宽为(a+b)米的长方形地块,规划部门计划将阴影部分进行绿化,中间将搞一雕塑. 如图,有一个圆锥形粮堆,正三角形ABC的边长为6m,粮堆母线AC的中点P处有一只鼠正在吃粮食,此时小猫正在B处,它要沿圆锥侧面P处捉老鼠,小猫所经过的最短路程是
如图,有一个圆锥形粮堆,正三角形ABC的边长为6m,粮堆母线AC的中点P处有一只鼠正在吃粮食,此时小猫正在B处,它要沿圆锥侧面P处捉老鼠,小猫所经过的最短路程是 如图,O是△ABC内一点,∠ACB=60°,∠α=∠β,则∠O=
如图,O是△ABC内一点,∠ACB=60°,∠α=∠β,则∠O= 如图,在△ABC中,E、F分别是AB、BC的中点,M、N是AC的三等分点,EM、FN的延长线相交于点D.求证:四边形ABCD是平行四边形.
如图,在△ABC中,E、F分别是AB、BC的中点,M、N是AC的三等分点,EM、FN的延长线相交于点D.求证:四边形ABCD是平行四边形.