题目内容
3.已知:如图1,△ABC和△CDE都是等腰直角三角形,且∠ACB=∠DCE=90°,O,M,N分别为AB,AD,BE的中点,连接OM,ON,MN.(1)求证:OM=ON,OM⊥ON.
(2)将图1中△CDE绕点C逆时针旋转得图2,记旋转角为α(0°<α<180°).已知BC=2CD=6,求在旋转过程中线段MN的最小值.
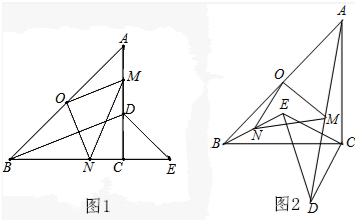
分析 (1)连结OC,如图1,根据AC=BC,CD=CE,M,N分别为AD,BE的中点,利用等线段代换可证明AM=CN,再根据三角形三角形斜边上的中线性质得到OC=OA,∠BOC=∠A=45°,∠AOC=90°,于是可根据“SAS”判断△OCN≌△OAM,则ON=OM,∠CON=∠AOM,然后证明∠MON=90°得到OM⊥ON;
(2)连结BD,如图2,先判断△OMN为等腰直角三角形得到MN=$\sqrt{2}$OM,再判断OM为△ABD的中位线得到OM=$\frac{1}{2}$BD,则MN=$\frac{\sqrt{2}}{2}$BD,所以当BD的长最小时,MN的长最小,由于点D在以C点为圆心,CD为半径的圆上,则可判断点B到⊙C的最短距离就是BD的最小值,此时点D在BC上,所以BD的最小值为3,则MN的最小值为$\frac{3\sqrt{2}}{2}$.
解答 (1)证明: 连结OC,如图1,
连结OC,如图1,
∵△ABC和△CDE都是等腰直角三角形,
∴AC=BC,CD=CE,
∵M,N分别为AD,BE的中点,
∴AM=$\frac{1}{2}$AD=$\frac{1}{2}$(AC-CD)=$\frac{1}{2}$(BC-CE)=$\frac{1}{2}$(BN+CN-CE)=$\frac{1}{2}$(NE+CN-CE)=$\frac{1}{2}$(NC+CE+CN-CE)=CN,
∵点O为等腰直角三角形斜边AB的中点,
∴OC=OA,∠BOC=∠A=45°,∠AOC=90°,
在△OCN和△OAM中
$\left\{\begin{array}{l}{OC=OA}\\{∠OCN=∠A}\\{CN=AM}\end{array}\right.$,
∴△OCN≌△OAM,
∴ON=OM,∠CON=∠AOM,
∵∠AOM+∠COM=90°,
∴∠COM+∠CON=90°,即∠MON=90°,
∴OM⊥ON;
(2)解:连结BD,如图2,
∵OM=ON,∠MON=90°,
∴△OMN为等腰直角三角形,
∴MN=$\sqrt{2}$OM,
∵点O、M分别为AB、AD的中点,
∴OM为△ABD的中位线,
∴OM=$\frac{1}{2}$BD,
∴MN=$\frac{\sqrt{2}}{2}$BD,
当BD的长最小时,MN的长最小,
∵点D在以C点为圆心,CD为半径的圆上,
∴点B到⊙C的最短距离就是BD的最小值,此时点D在BC上,
∵BC=2CD=6,
∴BD的最小值为3,
∴MN的最小值为$\frac{3\sqrt{2}}{2}$.
点评 本题考查了旋转的性质:对应点到旋转中心的距离相等;对应点与旋转中心所连线段的夹角等于旋转角;旋转前、后的图形全等.解决本题的关键是灵活应用等腰直角三角形的性质.

 阅读快车系列答案
阅读快车系列答案 在Rt△ABC中,∠C=90°,AC=8,BC=6,将其如图折叠使点A与点B重合,折痕为DE,连接BE,则tan∠CBE的值为( )
在Rt△ABC中,∠C=90°,AC=8,BC=6,将其如图折叠使点A与点B重合,折痕为DE,连接BE,则tan∠CBE的值为( )| A. | $\frac{24}{7}$ | B. | $\frac{\sqrt{7}}{3}$ | C. | $\frac{7}{24}$ | D. | $\frac{1}{3}$ |
 如图,已知点A(0,1),B(0,-1),以点A为圆心,AB为半径作圆,交x轴于点C和点D,则DC的长为( )
如图,已知点A(0,1),B(0,-1),以点A为圆心,AB为半径作圆,交x轴于点C和点D,则DC的长为( )| A. | 2 | B. | 4 | C. | $\sqrt{3}$ | D. | 2$\sqrt{3}$ |
| A. | 猴 | B. | 年 | C. | 吉 | D. | 祥 |

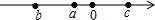 已知实数a,b,c在数轴上的位置如图所示,则化简$\sqrt{{a}^{2}}$-$\sqrt{(a-b)^{2}}$-$\sqrt{(a-c)^{2}}$-$\sqrt{(b-c)^{2}}$的结果是( )
已知实数a,b,c在数轴上的位置如图所示,则化简$\sqrt{{a}^{2}}$-$\sqrt{(a-b)^{2}}$-$\sqrt{(a-c)^{2}}$-$\sqrt{(b-c)^{2}}$的结果是( )