题目内容
 已知二次函数y=x2+bx+c的图象经过点(-4,3)、(-3,0).
已知二次函数y=x2+bx+c的图象经过点(-4,3)、(-3,0).(1)求b、c的值;
(2)画出该函数的图象;
(3)若x>m时,y随x的增大而增大,则m的最小值为
(4)该函数图象向上平移
考点:待定系数法求二次函数解析式,二次函数的图象,二次函数图象与几何变换,二次函数的最值
专题:计算题
分析:(1)把已知两点坐标代入二次函数解析式求出b与c的值即可;
(2)画出函数图象,如图所示;
(3)利用二次函数的性质判断即可确定出m的值;
(4)利用平移规律判断即可.
(2)画出函数图象,如图所示;
(3)利用二次函数的性质判断即可确定出m的值;
(4)利用平移规律判断即可.
解答:解:(1)把(-4,3)与(-3,0)代入得:
,
解得:b=4,c=3;
(2)二次函数解析式为y=x2+4x+3=(x+2)2-1,即顶点(-2,-1),
列表得:
描点;
连线,
如图所示:

(3)若x>m时,y随x的增大而增大,则m的最小值为-2;
(4)该函数图象向上平移1个单位长度后,所得函数的图象与x轴只有一个公共点.
故答案为:(3)-2;(4)1
|
解得:b=4,c=3;
(2)二次函数解析式为y=x2+4x+3=(x+2)2-1,即顶点(-2,-1),
列表得:
| x | 0 | -1 | -2 | -3 | -4 |
| y | 3 | 0 | -1 | 0 | 3 |
连线,
如图所示:

(3)若x>m时,y随x的增大而增大,则m的最小值为-2;
(4)该函数图象向上平移1个单位长度后,所得函数的图象与x轴只有一个公共点.
故答案为:(3)-2;(4)1
点评:此题考查了待定系数法求二次函数解析式,以及二次函数的图象与性质,熟练掌握待定系数法是解本题的关键.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
 如图,线段AD到线段BC的运动可能是( )
如图,线段AD到线段BC的运动可能是( )| A、向上平移2格,再向右平移3格 |
| B、向上平移2格,再向左平移1格 |
| C、向上平移1格,再向左平移2格 |
| D、向上平移1格,再向右平移3格 |
将一个正方形剪成n个小正方形,第一次操作按照图1所示,分割出4个正方形,第二次操作按如图2所示,分割出6个正方形,第三次操作按如图3所示,按照上述规律,则第n次操作,正方形的个数为( )
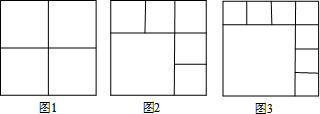

| A、(n+1)2 |
| B、3n+1 |
| C、2n |
| D、2n+2 |
 如图,A,B,C是⊙O上的三个点,如果∠BAC=30°,那么∠BOC的度数是( )
如图,A,B,C是⊙O上的三个点,如果∠BAC=30°,那么∠BOC的度数是( )| A、60° | B、45° |
| C、30° | D、15° |
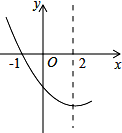 如图,是抛物线y=ax2+bx+c(a≠0)图象的一部分.已知抛物线的对称轴为x=2,与x轴的一个交点是(-1,0).有下列结论:①abc>0;②4a-2b+c<0;③b2-4ac>0’④点(-2,y1),(3,y2)都在抛物线上,则有y1<y2;⑤关于x的方程ax2+bx+c=0的解是-1和5.其中正确的是( )
如图,是抛物线y=ax2+bx+c(a≠0)图象的一部分.已知抛物线的对称轴为x=2,与x轴的一个交点是(-1,0).有下列结论:①abc>0;②4a-2b+c<0;③b2-4ac>0’④点(-2,y1),(3,y2)都在抛物线上,则有y1<y2;⑤关于x的方程ax2+bx+c=0的解是-1和5.其中正确的是( )| A、①②③ | B、②④⑤ |
| C、①③⑤ | D、③④ |
函数:①y=
;②y=
;③y=2x+3;④y=-x2;⑤y=
-x,其中y是x的一次函数的个数为( )
| x |
| 3 |
| 1 |
| x |
| 1 |
| 2 |
| A、2个 | B、3个 | C、4个 | D、5个 |
设p=
-
,q=
-
,则p,q的关系是( )
| a |
| a+1 |
| b |
| b+1 |
| 1 |
| a+1 |
| 1 |
| b+1 |
| A、p=q | B、p>q |
| C、p<q | D、p=-q |
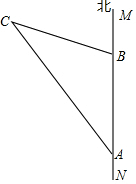 如图,直线MN是沿海边南北方向的一条公路,某施工队在公路的A点测得北偏西30°的方向上有一栋别墅C,沿正北方向走了400米到达B点后,测得别墅C在北偏西75°的方向上,现要从别墅C修一条通向公路MN的最短的小路,请你求出这条小路的长.
如图,直线MN是沿海边南北方向的一条公路,某施工队在公路的A点测得北偏西30°的方向上有一栋别墅C,沿正北方向走了400米到达B点后,测得别墅C在北偏西75°的方向上,现要从别墅C修一条通向公路MN的最短的小路,请你求出这条小路的长.