题目内容
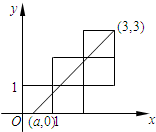五个边长为1的正方形如图摆放在平面直角坐标系中，经过（a，0），（3，3）的一条直线将这五个正方形分成面积相等的两部分，则a的值是
- A.
- B.
- C.
- D.
D
分析：首先作CB⊥x轴于B，作CD⊥y轴于D，然后根据题意即可得：S梯形OACD-3=S△ABC-1，又由经过（a，0），（3，3），即可得方程：
-3=
-1，解此方程即可求得答案．
解答：
解：如图：作CB⊥x轴于B，作CD⊥y轴于D，
根据题意得：S梯形OACD-3=S△ABC-1，
∵A（a，0），B（3，3），
∴CD=BC=OD=OB=3，OA=a，
∴AB=3-a，
∴-3=-1，
解得：a=．
故选D．
点评：此题考查了面积相等问题．此题难度较大，解题的关键是作CB⊥x轴，作CD⊥y轴，根据题意即得到：S梯形OACD-3=S△ABC-1，然后利用方程求解．
分析：首先作CB⊥x轴于B，作CD⊥y轴于D，然后根据题意即可得：S梯形OACD-3=S△ABC-1，又由经过（a，0），（3，3），即可得方程：
-3=-1，解此方程即可求得答案．解答：
解：如图：作CB⊥x轴于B，作CD⊥y轴于D，根据题意得：S梯形OACD-3=S△ABC-1，
∵A（a，0），B（3，3），
∴CD=BC=OD=OB=3，OA=a，
∴AB=3-a，
∴
-3=-1，解得：a=
．故选D．
点评：此题考查了面积相等问题．此题难度较大，解题的关键是作CB⊥x轴，作CD⊥y轴，根据题意即得到：S梯形OACD-3=S△ABC-1，然后利用方程求解．
练习册系列答案
相关题目
如图是由五个边长为1的正方形组成的图形，过点A的一条直线和ED，CD分别交于点M，N，假若直线MN在绕点A转动的过程中，存在某一位置，使得直线两侧的图形有相等的面积，则此时PM的长为
如图，由五个边长为1cm的正方形组成的图形中，过点A的一条直线l与ED、CD分别交于M、N，若直线l将图形分为面积相等的两部分，则EM=
如图，平面直角坐标系中的图案是由五个边长为1的正方形组成的．A（a，0），B（3，3），连接AB的线段将图案的面积分成相等的两部分，则a的值是
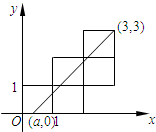五个边长为1的正方形如图摆放在平面直角坐标系中，经过（a，0），（3，3）的一条直线将这五个正方形分成面积相等的两部分，则a的值是（ ）A、
| ||
B、
| ||
C、
| ||
D、
|