题目内容
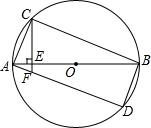 如图,矩形ABCD,AB是⊙O的直径,CE⊥AB,垂足为E,交AD于F,求证:AC2=AF•AD.
如图,矩形ABCD,AB是⊙O的直径,CE⊥AB,垂足为E,交AD于F,求证:AC2=AF•AD.考点:相似三角形的判定与性质,圆周角定理
专题:证明题
分析:连接CD,由圆周角定理可得∠ADC=∠ABC,再根据直角三角形的性质得出∠ACE=∠ABC,故可得出∠ADC=∠ACE,所以△ACF∽△ADC,故可得出结论.
解答: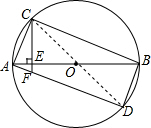 证明:连接CD,
证明:连接CD,
∵∠ADC与∠ABC是同弧所对的圆周角,
∴∠ADC=∠ABC.
∵AB是⊙O的直径,CE⊥AB,
∴∠ACB=∠AEC=90°,
∴∠CAB∠ABC=90°,∠CAB+∠ACE=90°,
∴∠ADC=∠ACE,
∴△ACF∽△ADC,
∴
=
,即AC2=AF•AD.
 证明:连接CD,
证明:连接CD,∵∠ADC与∠ABC是同弧所对的圆周角,
∴∠ADC=∠ABC.
∵AB是⊙O的直径,CE⊥AB,
∴∠ACB=∠AEC=90°,
∴∠CAB∠ABC=90°,∠CAB+∠ACE=90°,
∴∠ADC=∠ACE,
∴△ACF∽△ADC,
∴
| AC |
| AD |
| AF |
| AC |
点评:本题主要考查了圆周角定理和相似三角形的判定和性质等知识点.通过构建与所求相关的相等角是解题的关键.

练习册系列答案
 本土教辅赢在暑假高效假期总复习云南科技出版社系列答案
本土教辅赢在暑假高效假期总复习云南科技出版社系列答案 暑假作业北京艺术与科学电子出版社系列答案
暑假作业北京艺术与科学电子出版社系列答案 第三学期赢在暑假系列答案
第三学期赢在暑假系列答案
相关题目
在平面直角坐标系中,点P(x,y),其中xy>0,x>y,且点P到x轴、y轴的距离分别为6和2,则点P的坐标为( )
| A、(2,6) |
| B、(-6,-2) |
| C、(6,2) |
| D、(-2,-6) |
 以下四个三角形,与如图的三角形相似的是( )
以下四个三角形,与如图的三角形相似的是( )A、 |
B、 |
C、 |
D、 |
 如图所示,最外侧大圆的面积是半径为2厘米的小圆面积的几倍?阴影部分的面积是半径为3厘米的圆的面积的多少?
如图所示,最外侧大圆的面积是半径为2厘米的小圆面积的几倍?阴影部分的面积是半径为3厘米的圆的面积的多少? 如图,△ABC为等腰直角三角形,∠BAC=90°,在边BC上取点D,使BD=2DC,BE⊥AD交AC于E,垂足为F.求证:AE=EC.
如图,△ABC为等腰直角三角形,∠BAC=90°,在边BC上取点D,使BD=2DC,BE⊥AD交AC于E,垂足为F.求证:AE=EC.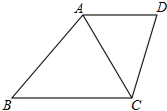 如图,在梯形ABCD中,AD∥BC,∠B=∠ACD,若AC=12,BC=16.
如图,在梯形ABCD中,AD∥BC,∠B=∠ACD,若AC=12,BC=16. 如图,在Rt△ABC中,以点C为圆心,BC为半径的圆交AB于点D,交AC于点E,∠BCD=40°,则∠A=
如图,在Rt△ABC中,以点C为圆心,BC为半径的圆交AB于点D,交AC于点E,∠BCD=40°,则∠A=