题目内容
 如图,△ABC为等腰直角三角形,∠BAC=90°,在边BC上取点D,使BD=2DC,BE⊥AD交AC于E,垂足为F.求证:AE=EC.
如图,△ABC为等腰直角三角形,∠BAC=90°,在边BC上取点D,使BD=2DC,BE⊥AD交AC于E,垂足为F.求证:AE=EC.考点:相似三角形的判定与性质,全等三角形的判定与性质
专题:证明题
分析:作AC⊥CG交AD的延长线于点G,则可证明△ABE≌△CAG,可得到AE=GC,再证明△ABD∽△CGD,利用相似比可得到AB=2CG,结合条件可得到AC=2AE,即AE=EC.
解答: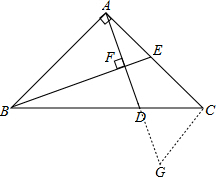 证明:作AC⊥CG交AD的延长线于点G,
证明:作AC⊥CG交AD的延长线于点G,
∵BE⊥AD,∠BAC=90°,
∴∠CAG+∠BAG=∠ABE+∠BAG=90°,
∴∠CAG=∠ABE,
在△ABE和△CAG中,
,
∴△ABE≌△CAG(AAS),
∴AE=GC,
∵AB⊥AC,GC⊥AC,
∴AB∥CG,
∴
=
=2,
∴AB=2GC,
∵CG=AE,AB=AC,
∴AC=2AE,
∴AE=EC.
 证明:作AC⊥CG交AD的延长线于点G,
证明:作AC⊥CG交AD的延长线于点G,∵BE⊥AD,∠BAC=90°,
∴∠CAG+∠BAG=∠ABE+∠BAG=90°,
∴∠CAG=∠ABE,
在△ABE和△CAG中,
|
∴△ABE≌△CAG(AAS),
∴AE=GC,
∵AB⊥AC,GC⊥AC,
∴AB∥CG,
∴
| AB |
| CG |
| BD |
| CD |
∴AB=2GC,
∵CG=AE,AB=AC,
∴AC=2AE,
∴AE=EC.
点评:本题主要考查全等三角形的判定和性质及平行线分线段成比例的性质,由全等得到AE=CG,再由相似找到AC与CG的关系是解题的关键,注意全等三角形、相似三角形的性质的应用.

练习册系列答案
 每日10分钟口算心算速算天天练系列答案
每日10分钟口算心算速算天天练系列答案
相关题目
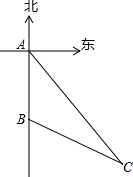 某次台风袭击了我国西南部海域.如图,台风来临前,我国海上搜救中心A接到一渔船遇险的报警,于是令位于A的正南方向180海里的救援队B立即施救.已知渔船所处位置C在A的南偏东34°方向,在B的南偏东63°方向,此时离台风来到C处还有12小时,如果救援船每小时行驶20海里,试问能否在台风来到之前赶到C处对其施救?
某次台风袭击了我国西南部海域.如图,台风来临前,我国海上搜救中心A接到一渔船遇险的报警,于是令位于A的正南方向180海里的救援队B立即施救.已知渔船所处位置C在A的南偏东34°方向,在B的南偏东63°方向,此时离台风来到C处还有12小时,如果救援船每小时行驶20海里,试问能否在台风来到之前赶到C处对其施救?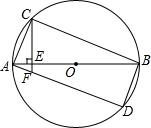 如图,矩形ABCD,AB是⊙O的直径,CE⊥AB,垂足为E,交AD于F,求证:AC2=AF•AD.
如图,矩形ABCD,AB是⊙O的直径,CE⊥AB,垂足为E,交AD于F,求证:AC2=AF•AD. △ABC中,D为BC边的中点,延长AD至E、延长AB交CE于P,若AD=2DE,求证:AP=3AB.
△ABC中,D为BC边的中点,延长AD至E、延长AB交CE于P,若AD=2DE,求证:AP=3AB.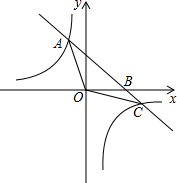 如图,已知直线y=-x+4与反比例函数y=
如图,已知直线y=-x+4与反比例函数y=