题目内容
4.以二元一次方程的解为坐标的点的全体叫做二元一次方程的图象,例如:以方程x-2y=1的解为坐标的点的全体叫做方程x-2y=1的图象;一般地,任何一个二元一次方程分图象都是一条直线,根据上述描述,做下列题目:有两个二元一次方程:ax-y+b=0和cx-y+5=0,学生甲子啊画出这两个二元一次方程的图象时,发现它们的交点为(3,2),学生乙因把c抄错而发现它们的交点为($\frac{3}{4}$,$\frac{1}{4}$),请求出a和b的值.分析 根据函数图象交点坐标为两函数解析式组成的方程组的解,把(3,2)和($\frac{3}{4}$,$\frac{1}{4}$)分别代入ax-y+b=0中得到关于a、b的方程组,然后解方程组即可.
解答 解:∵直线ax-y+b=0和cx-y+5=0的交点为(3,2),
∴3a-2+b=0①,
∵点($\frac{3}{4}$,$\frac{1}{4}$)在直线ax-y+b=0上,
∴$\frac{3}{4}$a-$\frac{1}{4}$+b=0②,
①-②得3a-$\frac{3}{4}$a-2+$\frac{1}{4}$=0,
解得a=$\frac{7}{9}$,
把a=$\frac{7}{9}$代入①得$\frac{7}{3}$-2+b=0,
解得b=-$\frac{1}{3}$.
答:a和b的值分别为$\frac{7}{9}$,-$\frac{1}{3}$.
点评 本题考查了一次函数与二元一次方程(组):函数图象交点坐标为两函数解析式组成的方程组的解.

练习册系列答案
相关题目
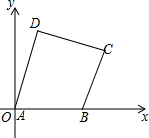 如图,在平面直角坐标系中,四边形各顶点的坐标分别为:A(0,0),B(7,0),C(9,5),D(2,7)
如图,在平面直角坐标系中,四边形各顶点的坐标分别为:A(0,0),B(7,0),C(9,5),D(2,7) 如图所示,在菱形ABCD中,AB=4,∠BAD=120°,点E、F分别在菱形的边BC、CD上运动,且∠EAF=60°且E、F不与B、C、D重合,连接AC交EF于P点.
如图所示,在菱形ABCD中,AB=4,∠BAD=120°,点E、F分别在菱形的边BC、CD上运动,且∠EAF=60°且E、F不与B、C、D重合,连接AC交EF于P点. 在如图所示的平面直角坐标系中,描出下列各点,再依次连接各点,构成封闭图形,A(-4,3),B(4,3),C(4,-3),D(-4,-3).回答下列问题:
在如图所示的平面直角坐标系中,描出下列各点,再依次连接各点,构成封闭图形,A(-4,3),B(4,3),C(4,-3),D(-4,-3).回答下列问题: