题目内容
1.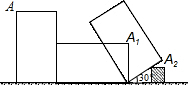 如图,小虎使一长为4cm,宽为2cm的长方形木板,在桌面上做无滑动的翻滚(顺时针方向)木板上点A位置变化为A→A1→A2,其中第二次翻滚被桌面上一小木块挡住,使木板与桌面成30°角.若连接AA2,则线段AA2的长(精确到0.1)约为( )
如图,小虎使一长为4cm,宽为2cm的长方形木板,在桌面上做无滑动的翻滚(顺时针方向)木板上点A位置变化为A→A1→A2,其中第二次翻滚被桌面上一小木块挡住,使木板与桌面成30°角.若连接AA2,则线段AA2的长(精确到0.1)约为( )| A. | 7.7cm | B. | 8.3cm | C. | 10.7cm | D. | 68.8cm |
分析 作A2B⊥AD,A2C⊥DE,在直角△ABA2中利用勾股定理即可求解.
解答  解:作A2B⊥AD,A2C⊥DE.
解:作A2B⊥AD,A2C⊥DE.
直角△A2EC中,A2C=AE•sin30°=2×$\frac{1}{2}$=1,EC=A2E•cos30°=$\sqrt{3}$.
则A2E=2+4+$\sqrt{3}$=6+$\sqrt{3}$.AB=4-1=3.
在直角△ABA2中,AA2=$\sqrt{A{B}^{2}+{A}_{2}{B}^{2}}$=$\sqrt{{3}^{2}+(6+\sqrt{3})^{2}}$=$\sqrt{48+12\sqrt{3}}$≈8.3(cm).
故选B.
点评 本题考查了解直角三角形的应用,正确作出辅助线,构造直角三角形是关键.

练习册系列答案
相关题目
6. 如图,将周长为10的△ABC沿BC方向平移l个单位,得到△DEF,则四边形ABFD的周长是( )
如图,将周长为10的△ABC沿BC方向平移l个单位,得到△DEF,则四边形ABFD的周长是( )
 如图,将周长为10的△ABC沿BC方向平移l个单位,得到△DEF,则四边形ABFD的周长是( )
如图,将周长为10的△ABC沿BC方向平移l个单位,得到△DEF,则四边形ABFD的周长是( )| A. | 12 | B. | 14 | C. | 15 | D. | 16 |
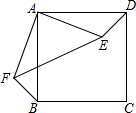 如图,将正方形ABCD中的△ADE绕着点A顺时针旋转与△ABF重合,若AE=4,则EF的长为4$\sqrt{2}$.
如图,将正方形ABCD中的△ADE绕着点A顺时针旋转与△ABF重合,若AE=4,则EF的长为4$\sqrt{2}$.