题目内容
10.(1)若等腰三角形有两条边的长度为3和1,则此等腰三角形的周长为7;(2)在等腰△ABC中,∠A=40°,且AB=BC,则∠B=100°.
分析 (1)分3是底边和腰长两种情况讨论求解,再根据三角形的三边关系判断是否能组成三角形;
(2)根据等边对等角可得∠A=∠C,然后根据三角形的内角和等于180°列式计算即可得解.
解答 解:(1)①若3是底边,则腰长为1,三角形的三边分别为3、1、1,
∵1+1=2<3,
∴不能组成三角形,
②若3是腰长,则底边为1,三角形的三边分别为3、3、1,
能组成三角形,
周长=3+3+1=7,
综上所述,此等腰三角形的周长为7;
(2)∵AB=BC,
∴∠A=∠C=40°,
∴∠B=180°-∠A-∠C=180°-40°-40°=100°.
故答案为:(1)7;(2)100°.
点评 本题考查了等腰三角形的性质,等边对等角的性质,三角形的内角和定理,难点在于分情况讨论.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
1.±4是16的( )
| A. | 平方根 | B. | 算术平方根 | C. | 相反数 | D. | 绝对值 |
15.下列各组数中,互为相反数的一组是( )
| A. | -|-2|与$\root{3}{-8}$ | B. | -4与-$\sqrt{(-4)^{2}}$ | C. | -$\root{3}{2}$与$\root{3}{2}$ | D. | -$\sqrt{2}$与-$\sqrt{(-2)^{2}}$ |
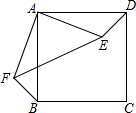 如图,将正方形ABCD中的△ADE绕着点A顺时针旋转与△ABF重合,若AE=4,则EF的长为4$\sqrt{2}$.
如图,将正方形ABCD中的△ADE绕着点A顺时针旋转与△ABF重合,若AE=4,则EF的长为4$\sqrt{2}$.