题目内容
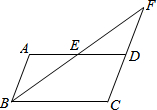 如图,在?ABCD中,AB=AE,连接BE且延长CD的延长线于点F.求证:AD=CF.
如图,在?ABCD中,AB=AE,连接BE且延长CD的延长线于点F.求证:AD=CF.考点:平行四边形的性质
专题:证明题
分析:利用平行四边形的性质得出AD∥BC,AB∥FC,AD=BC,进而得出∠CBF=∠F,即可得出AD=CF.
解答:证明:∵四边形ABCD是平行四边形,
∴AD∥BC,AB∥FC,AD=BC,
∴∠ABE=∠F,∠CBE=∠FED,
∵AB=AE,
∴∠ABE=∠AEB,
∴∠CBF=∠F,
∴BC=FC,
∴AD=CF.
∴AD∥BC,AB∥FC,AD=BC,
∴∠ABE=∠F,∠CBE=∠FED,
∵AB=AE,
∴∠ABE=∠AEB,
∴∠CBF=∠F,
∴BC=FC,
∴AD=CF.
点评:此题主要考查了平行四边形的性质,利用平行线的性质得出∠CBF=∠F是解题关键.

练习册系列答案
相关题目
 如图,在Rt△ABC中,∠ACB=90°,CD⊥AB于点D,如果AC=3,AB=6,那么AD的值为( )
如图,在Rt△ABC中,∠ACB=90°,CD⊥AB于点D,如果AC=3,AB=6,那么AD的值为( )A、
| ||||
B、
| ||||
C、
| ||||
D、3
|
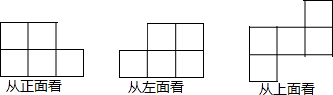 如图是由几个完全相同的小正方形搭成的几何体从正面、左面、上面看到的形状图,则搭成这样的几何体所用的小正方形的个数最少是( )
如图是由几个完全相同的小正方形搭成的几何体从正面、左面、上面看到的形状图,则搭成这样的几何体所用的小正方形的个数最少是( )| A、8个 | B、7个 | C、6个 | D、5个 |
二次函数y=-(x-3)2+1的最大值为( )
| A、1 | B、-1 | C、3 | D、-3 |




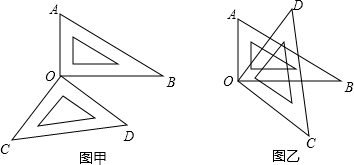
 如图,已知∠EOC是平角,OD平分∠BOC,在平面上画射线OA,使∠AOC和∠COD互余,若∠BOC=50°,则∠AOB是
如图,已知∠EOC是平角,OD平分∠BOC,在平面上画射线OA,使∠AOC和∠COD互余,若∠BOC=50°,则∠AOB是