题目内容
10．（1）用配方法解方程x2+6x-5=0（2）用适当的方法解方程：3（x-5）2=2（5-x）
分析 （1）配方法求解可得；
（2）因式分解法求解可得．
解答 解：（1）∵x2+6x=5，
∴x2+6x+9=5+9，即（x+3）2=14，
∴x+3=±$\sqrt{14}$，
则x=-3$±\sqrt{14}$；
（2）∵3（x-5）2+2（x-5）=0，
∴（x-5）[3（x-5）+2]=0，即（x-5）（3x-13）=0，
则x-5=0或3x-13=0，
解得：x=5或x=$\frac{13}{3}$．
点评 本题主要考查解一元二次方程的能力，熟练掌握解一元二次方程的几种常用方法：直接开平方法、因式分解法、公式法、配方法，结合方程的特点选择合适、简便的方法是解题的关键．
练习册系列答案
相关题目
如图，AC∥EF，AC=EF，AE=BD．求证：∠CBA=∠D．
1．小明靠勤工俭学的收入维持上大学的费用，下表是他在二月份一周的收支情况，规定收入为正，支出为负（单位：元）
（1）哪天的收入小于支出？答：周六；
（2）求小明在一周内有多少节余？
（3）按以上支出，小明二月份（按28天计算）至少要赚多少钱，才得以维持正常开支？
| 周一 | 周二 | 周三 | 周四 | 周五 | 周六 | 周日 |
| +15 | +12 | 0 | +20 | +15 | +10 | +14 |
| -8 | -12 | -19 | -10 | -9 | -11 | -8 |
（2）求小明在一周内有多少节余？
（3）按以上支出，小明二月份（按28天计算）至少要赚多少钱，才得以维持正常开支？
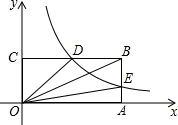如图，在平面直角坐标系中，点O为坐标原点，矩形OABC的边OA，OC分别在x轴和y轴上，其中OA=6，OC=3．已知反比例函数y=$\frac{k}{x}$（x＞0）的图象经过BC边上的中点D，交AB于点E．
如图，在边长为1的正方形组成的网格中，△AOB的顶点均在格点上，点A、B的坐标分别是A（3，2），B（1，3），△AOB关于y轴对称的图形为△A1OB1．
20．
如图，在△ABC中，AB=AC，D，E两点分别在AC，BC上，BD是∠ABC的平分线，DE∥AB，若BE=5cm，CE=3cm，则△CDE的周长是（ ）
如图，在△ABC中，AB=AC，D，E两点分别在AC，BC上，BD是∠ABC的平分线，DE∥AB，若BE=5cm，CE=3cm，则△CDE的周长是（ ）| A． | 15cm | B． | 13cm | C． | 11cm | D． | 9cm |