题目内容
20. 如图,AC∥EF,AC=EF,AE=BD.求证:∠CBA=∠D.
如图,AC∥EF,AC=EF,AE=BD.求证:∠CBA=∠D.
分析 根据平行线的性质得到∠A=∠FED,根据线段的和差得到AB=DE,根据全等三角形的性质即可得到结论.
解答 证明:∵AC∥EF,
∴∠A=∠FED,
∵AE=BD,
∴AE+BE=BD+BE,
即AB=DE,
在△ABC与△EFD中,
$\left\{\begin{array}{l}{AC=EF}\\{∠A=∠FED}\\{AB=ED}\end{array}\right.$,
∴△ABC≌△EDF,
∴∠CBA=∠D.
点评 本题考查了全等三角形的判定与性质、等腰三角形的判定;证明三角形全等得出对应角相等是解决问题的关键.

练习册系列答案
 小天才课时作业系列答案
小天才课时作业系列答案 一课四练系列答案
一课四练系列答案 黄冈小状元满分冲刺微测验系列答案
黄冈小状元满分冲刺微测验系列答案 新辅教导学系列答案
新辅教导学系列答案 阳光同学一线名师全优好卷系列答案
阳光同学一线名师全优好卷系列答案
相关题目
10.从六边形的一个顶点,可以引( )条对角线.
| A. | 3 | B. | 4 | C. | 5 | D. | 6 |
8.连续抛掷一枚质地均匀的硬币三次,有“两次正面朝上一次反面朝上”的概率是( )
| A. | $\frac{1}{8}$ | B. | $\frac{1}{4}$ | C. | $\frac{3}{8}$ | D. | $\frac{1}{2}$ |
15.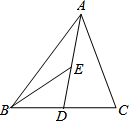 如图,BD=CD,AE=DE,△ABC的面积是4,则△ABE的面积是( )
如图,BD=CD,AE=DE,△ABC的面积是4,则△ABE的面积是( )
 如图,BD=CD,AE=DE,△ABC的面积是4,则△ABE的面积是( )
如图,BD=CD,AE=DE,△ABC的面积是4,则△ABE的面积是( )| A. | 2 | B. | 0.5 | C. | 1 | D. | 无法确定 |





 如图,已知AB=CD,AE=DF,BF=CE,求证∠B=∠C.
如图,已知AB=CD,AE=DF,BF=CE,求证∠B=∠C.