题目内容
17．下列长度的三条线段能组成锐角三角形的是（ ）| A． | 2，3，3 | B． | 2，3，4 | C． | 2，3，5 | D． | 3，4，5 |
分析 根据勾股定理求出以较短的两条边为直角边的三角形的斜边的长度，然后与较长的边进行比较作出判断即可．
解答 解：A、∵$\sqrt{{2}^{2}+{3}^{2}}$=$\sqrt{13}$＞3，2+3＞3，∴能组成锐角三角形；
B、∵$\sqrt{{2}^{2}+{3}^{2}}$=$\sqrt{13}$＜4，2+3＞4，∴不能组成锐角三角形；
C、∵2+3=5，∴不能组成三角形；
D、∵$\sqrt{{3}^{2}+{4}^{2}}$=5，是直角三角形，∴不能组成锐角三角形．
故选：A．
点评 本题考查了勾股定理的逆定理，利用勾股定理求出直角三角形的斜边是解题的关键．
练习册系列答案
阅读快车系列答案
相关题目
5．如果$\sqrt{3+a}$+（5-b）2=0，那么点A（a，b）关于原点对称的点A′的坐标为（ ）
| A． | （3，5） | B． | （3，-5） | C． | （-3，5） | D． | （5，-3） |
12．将直线y=2x-4向上平移5个单位长度后，所得直线的表达式是（ ）
| A． | y=2x-9 | B． | y=2x-5 | C． | y=2x+5 | D． | y=2x+1 |
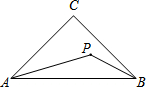如图，在△ABC中，∠C=90°，AC=BC=1，P为△ABC内一个动点，∠PAB=∠PBC，则CP的最小值为$\sqrt{2}$-1．
9．
如图，AB、CD相交于点O，EO⊥AB于O，则图中∠1与∠2的关系是（ ）
如图，AB、CD相交于点O，EO⊥AB于O，则图中∠1与∠2的关系是（ ）| A． | 互余的两角 | B． | 互补的两角 | C． | 对顶角 | D． | 一对相等的角 |