题目内容
15.有甲、乙两个不透明的布袋,甲袋中装有3个完全相同的小球,分别标有数字0,1,2;乙袋中装有3个完全相同的小球,分别标有数字-1,-2,0.现从甲袋中随机抽取一个小球,记录标有的数字为x,再从乙袋中随机抽取一个小球,记录标有数字为y,确定点M坐标为(x,y).(1)用树状图或列表法列举点M所有可能的坐标.
(2)求点M(x,y)在函数y=-x2-1的图象上的概率.
分析 (1)利用画树状图展示所有9种等可能的结果数;
(2)根据二次函数图象上点的坐标特征可判断点(0,-1),(1,-2)在函数y=-x2-1的图象上,然后根据概率公式求解.
解答 解:(1)画树状图为: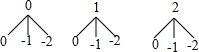
共有9种等可能的结果数;
(2)点M(x,y)在函数y=-x2-1的图象上的结果数为2,它们是(0,-1),(1,-2),
所以点M(x,y)在函数y=-x2-1的图象上的概率=$\frac{2}{9}$.
点评 本题考查了列表法与树状图法:通过列表法或树状图法展示所有等可能的结果求出n,再从中选出符合事件A或B的结果数目m,然后根据概率公式求出事件A或B的概率.也考查了二次函数图象上点的坐标特征.

练习册系列答案
相关题目
3.下列说法中正确的是( )
| A. | “任意画出一个等边三角形,它是轴对称图象”是随机事件 | |
| B. | 任意掷一枚质地均匀的硬币10次,正面向上的一定是5次 | |
| C. | “概率为0.0001的事件”是不可能事件 | |
| D. | “任意画出一个平行四边形,它是中心对称图形”是必然事件 |
20.在|-3|,0,-1,-2.5这四个有理数中,属于负整数的是( )
| A. | |-3| | B. | 0 | C. | -1 | D. | -2.5 |
14.下列长度的三根木棒首尾相接,能做成三角形框架的是( )
| A. | 1cm、2cm、3cm | B. | 2cm、3cm、4cm | C. | 4cm、9cm、4cm | D. | 2cm、1cm、4cm |
15. 在四边形ABCD中,AB∥CD,∠A=90°,AB=1,BD⊥BC,BD=BC,CF平分∠BCD交BD、AD于E、F,则△EDF的面积为( )
在四边形ABCD中,AB∥CD,∠A=90°,AB=1,BD⊥BC,BD=BC,CF平分∠BCD交BD、AD于E、F,则△EDF的面积为( )
 在四边形ABCD中,AB∥CD,∠A=90°,AB=1,BD⊥BC,BD=BC,CF平分∠BCD交BD、AD于E、F,则△EDF的面积为( )
在四边形ABCD中,AB∥CD,∠A=90°,AB=1,BD⊥BC,BD=BC,CF平分∠BCD交BD、AD于E、F,则△EDF的面积为( )| A. | 3$\sqrt{2}$-4 | B. | 3$\sqrt{2}$-3 | C. | 3$\sqrt{2}$-2 | D. | 3$\sqrt{2}$-1 |
 如图,已知△ABC中,∠C=90°,AC=BC=$\sqrt{2}$,将△ABC绕点A顺时针方向旋转60°到△AB1C1的位置,连接BC1并延长交AB1于点D,则BD的长为$\sqrt{3}$.
如图,已知△ABC中,∠C=90°,AC=BC=$\sqrt{2}$,将△ABC绕点A顺时针方向旋转60°到△AB1C1的位置,连接BC1并延长交AB1于点D,则BD的长为$\sqrt{3}$.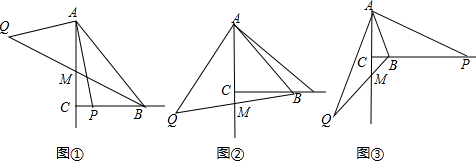
 如图有一块等腰梯形的空地ABCD,它的各边的中点分别是E,F,G,H,AC=20米.如果用篱笆将四边形EFGH的周长围起来,则共需要篱笆40米.
如图有一块等腰梯形的空地ABCD,它的各边的中点分别是E,F,G,H,AC=20米.如果用篱笆将四边形EFGH的周长围起来,则共需要篱笆40米.