题目内容
4.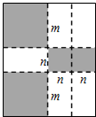 如图,将一张矩形大铁皮切割成九块,切痕如下图虚线所示,其中有两块是边长都为mcm的大正方形,两块是边长都为ncm的小正方形,五块是长宽分别是mcm、ncm的全等小矩形,且m>n.
如图,将一张矩形大铁皮切割成九块,切痕如下图虚线所示,其中有两块是边长都为mcm的大正方形,两块是边长都为ncm的小正方形,五块是长宽分别是mcm、ncm的全等小矩形,且m>n.(1)用含m、n的代数式表示切痕的总长为6m+6n cm;
(2)若每块小矩形的面积为48cm2,四个正方形的面积和为200cm2,试求该矩形大铁皮的周长.
分析 (1)根据切痕长有两横两纵列出算式,再根据合并同类项法则整理即可;
(2)根据小矩形的面积和正方形的面积列出算式,再利用完全平方公式整理求出m+n的值,然后根据矩形的周长公式整理求解即可.
解答 解:(1)切痕总长=2[(m+2n)+(2m+n)],
=2(m+2n+2m+n),
=6m+6n;
故答案为:6m+6n;
(2)由题意得:mn=48,2m2+2n2=200,
∴m2+n2=100,
∴(m+n)2=m2+n2+2mn=196,
∵m+n>0,
∴m+n=14,
∴周长=2(m+2n+2m+n)=6m+6n=6(m+n)=84.
点评 本题考查对完全平方公式几何意义的理解,应从整体和部分两方面来理解完全平方公式的几何意义;主要围绕图形周长和面积展开分析.

练习册系列答案
 亮点激活精编提优100分大试卷系列答案
亮点激活精编提优100分大试卷系列答案
相关题目
6.下列各式,是同类项的一组为( )
| A. | a2b与-ab2 | B. | xy2与-$\frac{3}{5}$y2x | C. | 5x与xy | D. | 5ab与6a2b |
7.下列变形符合等式基本性质的是( )
| A. | 如果2a-b=7,那么b=7-2a | B. | 如果mk=nk,那么m=n | ||
| C. | 如果-3x=5,那么x=5÷3 | D. | 如果-$\frac{1}{3}$a=2,那么a=-6 |
4.若3x=15,3y=5,则3x-y等于( )
| A. | 3 | B. | 5 | C. | 10 | D. | 12 |
11.在平面直角坐标系xOy中,y轴上有一点P,它到点A(4,3),B(3,-1)的距离之和最小,则点P的坐标是( )
| A. | (0,0) | B. | (0,$\frac{4}{7}$) | C. | (0,$\frac{5}{7}$) | D. | (0,$\frac{4}{5}$) |
9.若存在3个互不相同的实数a,b,c,使得|1-a|+|1-3a|+|1-4a|=|1-b|+|1-3b|+|1-4b|=|1-c|+|1-3c|+|1-4c|=t,则t=( )
| A. | 2 | B. | 1 | C. | -1 | D. | -2 |
16. 如图,线段AB、CD互相平分交于点O,则下列结论错误的是( )
如图,线段AB、CD互相平分交于点O,则下列结论错误的是( )
 如图,线段AB、CD互相平分交于点O,则下列结论错误的是( )
如图,线段AB、CD互相平分交于点O,则下列结论错误的是( )| A. | AD=BC | B. | ∠C=∠D | C. | AD∥BC | D. | OC=OB |
 如图所示,∠B=∠D=90°,BC=CD,∠1=30°,则∠2=60°.
如图所示,∠B=∠D=90°,BC=CD,∠1=30°,则∠2=60°. 八年级(3)班开展了手工制作竞赛,每个同学都在规定时间内完成一件手工作品.陈莉同学在制作手工作品的第一、二个步骤是:①先裁下了一张长BC=20cm,宽AB=16cm的矩形纸片ABCD,②将纸片沿着直线AE折叠,点D恰好落在BC边上的F处,则EC的长为6 cm.
八年级(3)班开展了手工制作竞赛,每个同学都在规定时间内完成一件手工作品.陈莉同学在制作手工作品的第一、二个步骤是:①先裁下了一张长BC=20cm,宽AB=16cm的矩形纸片ABCD,②将纸片沿着直线AE折叠,点D恰好落在BC边上的F处,则EC的长为6 cm.