题目内容
8.关于x的方程x+$\frac{1}{x}$=c+$\frac{1}{c}$的解是x1=c,x2=$\frac{1}{c}$,x-$\frac{1}{x}$=c-$\frac{1}{c}$(即x+$\frac{-1}{x}$=c+$\frac{-1}{c}$)的解释x1=c,x2=-$\frac{1}{c}$.
x+$\frac{2}{x}$=c+$\frac{2}{c}$的解释x1=c,x2=$\frac{2}{c}$
x+$\frac{3}{x}$=c+$\frac{3}{c}$的解是x1=c,x2=$\frac{3}{c}$…
(1)猜想关于x的方程x+$\frac{m}{x}$=c+$\frac{m}{c}$(m≠0)的解是什么,并利用“方程的解”的概念进行验证;
(2)利用你得到的结论解关于x的方程x+$\frac{2015}{x-1}$=a+$\frac{2015}{a-1}$.
分析 (1)根据已知方程的解猜想得到所求方程的解,验证即可;
(2)利用得出的结论求出所求方程的解即可.
解答 解:(1)猜想关于x的方程x+$\frac{m}{x}$=c+$\frac{m}{c}$(m≠0)的解是x1=c,x2=$\frac{m}{c}$,
把x=c代入方程得:左边=c+$\frac{m}{c}$,右边=c+$\frac{m}{c}$,左边=右边,即x=c是方程的解;
把x=$\frac{m}{c}$代入方程得:左边=$\frac{m}{c}$+$\frac{m}{\frac{m}{c}}$=c+$\frac{m}{c}$,右边=c+$\frac{m}{c}$,左边=右边,即x=$\frac{m}{c}$是方程的解;
(2)方程变形得:x-1+$\frac{2015}{x-1}$=a-1+$\frac{2015}{a-1}$,
根据题意得:x1=a,x2=$\frac{2015}{a-1}$+1,
点评 此题考查了分式方程的解,弄清题中的规律是解本题的关键.

练习册系列答案
 孟建平小学滚动测试系列答案
孟建平小学滚动测试系列答案 黄冈天天练口算题卡系列答案
黄冈天天练口算题卡系列答案
相关题目
20.下列说法正确的是( )
| A. | 6.4的立方根是0.4 | B. | -9的平方根是±3 | ||
| C. | $\sqrt{2}$是无理数 | D. | $\sqrt{3}$+$\sqrt{2}$=$\sqrt{5}$ |
18.下列图形不是正方体展开图的是( )
| A. |  | B. |  | C. |  | D. |  |
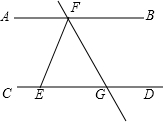 如图,AB∥CD,∠EFB=2∠DEF,FG平分∠EFB,则∠EGF=60°.
如图,AB∥CD,∠EFB=2∠DEF,FG平分∠EFB,则∠EGF=60°.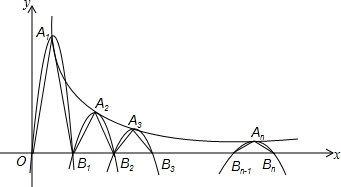 如图,一组抛物线的顶点A1(x1,y1),A2(x2,y2),…An(xn,yn)(n为正整数)依次是反比例函数y=$\frac{9}{x}$图象上的点,第一条抛物线以A1(x1,y1)为顶点且过点O(0,0),B1(2,0),等腰△A1OB1为第一个三角形;第二条抛物线以A2(x2,y2)为顶点且经过点B1(2,0),B2(4,0),等腰△A2B1B2为第二个三角形;…;第n条抛物线以An(xn,yn)为顶点且经过点Bn-1(2n-2,0),B2n(2n,0),等腰△AnBn-1Bn为第n个三角形.
如图,一组抛物线的顶点A1(x1,y1),A2(x2,y2),…An(xn,yn)(n为正整数)依次是反比例函数y=$\frac{9}{x}$图象上的点,第一条抛物线以A1(x1,y1)为顶点且过点O(0,0),B1(2,0),等腰△A1OB1为第一个三角形;第二条抛物线以A2(x2,y2)为顶点且经过点B1(2,0),B2(4,0),等腰△A2B1B2为第二个三角形;…;第n条抛物线以An(xn,yn)为顶点且经过点Bn-1(2n-2,0),B2n(2n,0),等腰△AnBn-1Bn为第n个三角形. 如图,AD=$\frac{1}{2}$DB,E是BC的中点,BE=$\frac{1}{5}$AC=2cm,则线段DE=6cm.
如图,AD=$\frac{1}{2}$DB,E是BC的中点,BE=$\frac{1}{5}$AC=2cm,则线段DE=6cm.