题目内容
16.若xy≠1,且有7x2+2009x+13=0及13y2+2009y+7=0,则$\frac{x}{y}$的值是( )| A. | $\frac{13}{7}$ | B. | $\frac{7}{13}$ | C. | -$\frac{2009}{7}$ | D. | -$\frac{2009}{13}$ |
分析 先把13y2+2009y+7=0变形得到7•($\frac{1}{y}$)2+2009•$\frac{1}{y}$+13=0,由于xy≠1,7x2+2009x+13=0,所以x和$\frac{1}{y}$可看作方程7z2+2009z+13=0的两根,然后根据根与系数的关系求解.
解答 解:∵13y2+2009y+7=0,y≠0,
∴7•($\frac{1}{y}$)2+2009•$\frac{1}{y}$+13=0,
∵xy≠1,7x2+2009x+13=0,
∴x和$\frac{1}{y}$可看作方程7z2+2009z+13=0的两根,
∴x•$\frac{1}{y}$=$\frac{13}{7}$,
即$\frac{x}{y}$的值为$\frac{13}{7}$.
点评 此题考查了一元二次方程ax2+bx+c=0(a≠0)的根与系数的关系:若方程两个为x1,x2,则x1+x2=-$\frac{b}{a}$,x1•x2=$\frac{c}{a}$.

练习册系列答案
相关题目
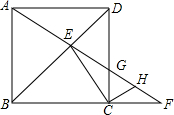 如图,在正方形ABCD中,F为BC的延长线上一点,AF交BD于点E,交CD于点G,求证:CE是△CGF外接圆的切线.
如图,在正方形ABCD中,F为BC的延长线上一点,AF交BD于点E,交CD于点G,求证:CE是△CGF外接圆的切线.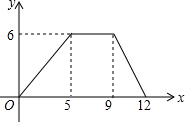 如图,是一对变量满足的函数关系的图象.有下列3个不同的问题情境:
如图,是一对变量满足的函数关系的图象.有下列3个不同的问题情境: 如图是由9个等边三角形拼成的六边形,若已知中间的小等边三角形的边长是2,则六边形的周长是60.
如图是由9个等边三角形拼成的六边形,若已知中间的小等边三角形的边长是2,则六边形的周长是60.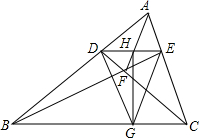 在△ABC中,D,E分别为AB,AC上一点,DE交AF于H,HG⊥BC,连接DG,GE.
在△ABC中,D,E分别为AB,AC上一点,DE交AF于H,HG⊥BC,连接DG,GE. 如图,在梯形ABCD中,AD∥BC,AB⊥BC,E是CD的中点,F在AB上,且∠1=∠2,AE、DF交于P,BE、CF交于Q,求证:四边形EPFQ是平行四边形.
如图,在梯形ABCD中,AD∥BC,AB⊥BC,E是CD的中点,F在AB上,且∠1=∠2,AE、DF交于P,BE、CF交于Q,求证:四边形EPFQ是平行四边形.