题目内容
6.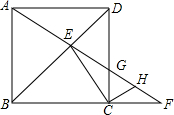 如图,在正方形ABCD中,F为BC的延长线上一点,AF交BD于点E,交CD于点G,求证:CE是△CGF外接圆的切线.
如图,在正方形ABCD中,F为BC的延长线上一点,AF交BD于点E,交CD于点G,求证:CE是△CGF外接圆的切线.
分析 通过全等三角形的判定定理SAS判定△DAE≌△DCE,然后根据全等三角形的对应角相等知∠DAE=∠DCE,由AD∥BF,求得∠DAE=∠F,∠GCF=∠ADC=90°,得出∠DCE=∠F,GF是△CGF外接圆的直径,从而求得GH=CH,根据等边对等角得出∠CGF=∠GCH,进而就可求得CH⊥CE,即可求得结论.
解答 证明:在△DAE和△DCE中,
∠ADE=∠CDE(正方形的对角线平分对角),
在△DAE和△DCE中,
$\left\{\begin{array}{l}{ED=ED}\\{∠ADE=∠CDE}\\{AD=CD}\end{array}\right.$,
∴△DAE≌△DCE (SAS),
∴∠DAE=∠DCE(全等三角形的对应角相等),
∵AD∥BF,
∴∠DAE=∠F,∠GCF=∠ADC=90°
∴∠DCE=∠F,GF是△CGF外接圆的直径,
∴圆心H是GF的中点,
∴GH=CH,
∴∠CGF=∠GCH,
∵∠F+∠CGF=90°,
∴∠GCE+∠GCH=90°,
∴CH⊥CE,
∴CE是△CGF外接圆的切线.
点评 本题考查了正方形的性质,三角形全等的判定和性质,圆周角定理以及切线的判定,熟练掌握性质定理是解题的关键.

练习册系列答案
相关题目
16.若xy≠1,且有7x2+2009x+13=0及13y2+2009y+7=0,则$\frac{x}{y}$的值是( )
| A. | $\frac{13}{7}$ | B. | $\frac{7}{13}$ | C. | -$\frac{2009}{7}$ | D. | -$\frac{2009}{13}$ |
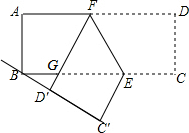 如图,矩形ABCD中,AB=4,AD=9,点E、F分别是BC、AD上的动点,∠FEC为钝角,沿直线EF翻折矩形,点C、D的对应点分别为C′、D′,若C′、D′、B在同一条直线上,且$\frac{BD′}{BC′}$=$\frac{1}{3}$时,则AF的长为3$\frac{5}{6}$.
如图,矩形ABCD中,AB=4,AD=9,点E、F分别是BC、AD上的动点,∠FEC为钝角,沿直线EF翻折矩形,点C、D的对应点分别为C′、D′,若C′、D′、B在同一条直线上,且$\frac{BD′}{BC′}$=$\frac{1}{3}$时,则AF的长为3$\frac{5}{6}$. 如图,如果AC∥BD,CE∥DF,那么△ACE与△BDF是位似三角形吗?为什么?
如图,如果AC∥BD,CE∥DF,那么△ACE与△BDF是位似三角形吗?为什么?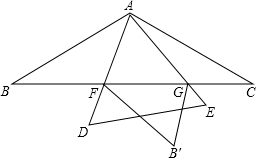 如图,△ABC中,AB=AC=4,∠BAC=120°,以A为一个顶点的等边三角形ADE绕点A在∠BAC内旋转,AD、AE所在的直线与BC边分别交于点F、G.若点B关于直线AD的对称点为B′,当△FGB′是以点G为直角顶点的直角三角形时,BF的长为4$\sqrt{3}$-4.
如图,△ABC中,AB=AC=4,∠BAC=120°,以A为一个顶点的等边三角形ADE绕点A在∠BAC内旋转,AD、AE所在的直线与BC边分别交于点F、G.若点B关于直线AD的对称点为B′,当△FGB′是以点G为直角顶点的直角三角形时,BF的长为4$\sqrt{3}$-4.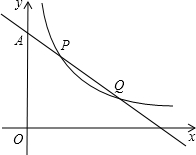 如图,反比例函数y1=$\frac{{k}_{1}}{x}$(x>0)的图象与直线y2=k2x+b交于P(3,7)、Q两点.
如图,反比例函数y1=$\frac{{k}_{1}}{x}$(x>0)的图象与直线y2=k2x+b交于P(3,7)、Q两点.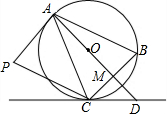 如图,AP是⊙O的切线,A为切点,AB是⊙O的弦,过点B作BC∥AP,交⊙O于点C,连接AC,过点C作CP∥AP于点P,连接AO并延长,交BC于点M,交过点C的直线于点D,且∠ACP=∠BCD
如图,AP是⊙O的切线,A为切点,AB是⊙O的弦,过点B作BC∥AP,交⊙O于点C,连接AC,过点C作CP∥AP于点P,连接AO并延长,交BC于点M,交过点C的直线于点D,且∠ACP=∠BCD