题目内容
12.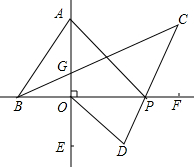 如图,直线AE⊥BF于O,将一个三角板ABO如图放置(∠BAO=30°),两直角边与直线BF,AE重合,P为直线BF上一动点,BC平分∠ABP,PC平分∠APF,OD平分∠POE.
如图,直线AE⊥BF于O,将一个三角板ABO如图放置(∠BAO=30°),两直角边与直线BF,AE重合,P为直线BF上一动点,BC平分∠ABP,PC平分∠APF,OD平分∠POE.(1)求∠BGO的度数;
(2)试确定∠C与∠OAP之间的数量关系并说明理由;
(3)P在直线上运动,∠C+∠D的值是否变化?若发生变化,说明理由;若不变求其值.
分析 (1)根据已知求出∠ABG的度数,运用外角的性质求出∠BGO的度数;
(2)根据外角的性质表示出∠C,得到∠C与∠OAP之间的数量关系;
(3)根据对顶角相等,分别表示出∠C和∠D,得到∠C+∠D的值.
解答 解:(1)∵∠BAO=30°,∴∠ABO=60°,∵BC平分∠ABP,∴∠ABG=∠GBO=30°,
∠BGO=∠BAG+∠ABG=60°.
(2)∠APF=∠OAP+∠AOP
∠C=$\frac{1}{2}$∠APF-∠CBF=$\frac{1}{2}$∠OAP+45°-30°=$\frac{1}{2}$∠OAP+15°
(3)∠C+∠D不变.
∠CPF=∠OPD,
∠CPF=∠C+30°,
∠OPD=180°-45°-∠D
∠C+30°=180°-45°-∠D
∠C+∠D=105°.
点评 本题考查的是三角形内角和定理、三角形的外角的性质、角平分线的定义,掌握定理、性质是解题的关键,解答时,注意结合图形正确写出各角之间的关系.

练习册系列答案
 津桥教育计算小状元系列答案
津桥教育计算小状元系列答案
相关题目
3.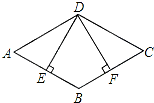 如图,菱形ABCD的边长为8cm,∠A=60°,DE⊥AB于点E,DF⊥BC于点F,则四边形BEDF的面积为( )cm2.
如图,菱形ABCD的边长为8cm,∠A=60°,DE⊥AB于点E,DF⊥BC于点F,则四边形BEDF的面积为( )cm2.
 如图,菱形ABCD的边长为8cm,∠A=60°,DE⊥AB于点E,DF⊥BC于点F,则四边形BEDF的面积为( )cm2.
如图,菱形ABCD的边长为8cm,∠A=60°,DE⊥AB于点E,DF⊥BC于点F,则四边形BEDF的面积为( )cm2.| A. | 16$\sqrt{3}$ | B. | 64 | C. | 8$\sqrt{3}$ | D. | 8 |
 如图,△ABC中,∠B=2∠C,AD⊥BC于D,M是BC的中点,求证:AB=2DM.
如图,△ABC中,∠B=2∠C,AD⊥BC于D,M是BC的中点,求证:AB=2DM.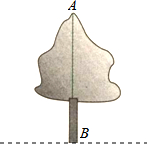 如图,要测量树AB的高,可以利用相似三角形的知识,请你设计几种测量方案,并说明每种方案的理由.
如图,要测量树AB的高,可以利用相似三角形的知识,请你设计几种测量方案,并说明每种方案的理由. 如图,正方形ABCD的顶点B,C在x轴的正半轴上,反比例函数y=$\frac{k}{x}$(k≠0)在第一象限的图象经过顶点A(m,m+1)和CD边上的点E的纵坐标为$\frac{2}{3}$,过点E的直线l交于x轴于点F,交y轴于点G(0,-2),则OB:BF:FC为( )
如图,正方形ABCD的顶点B,C在x轴的正半轴上,反比例函数y=$\frac{k}{x}$(k≠0)在第一象限的图象经过顶点A(m,m+1)和CD边上的点E的纵坐标为$\frac{2}{3}$,过点E的直线l交于x轴于点F,交y轴于点G(0,-2),则OB:BF:FC为( )