题目内容
2. 如图,正方形ABCD的顶点B,C在x轴的正半轴上,反比例函数y=$\frac{k}{x}$(k≠0)在第一象限的图象经过顶点A(m,m+1)和CD边上的点E的纵坐标为$\frac{2}{3}$,过点E的直线l交于x轴于点F,交y轴于点G(0,-2),则OB:BF:FC为( )
如图,正方形ABCD的顶点B,C在x轴的正半轴上,反比例函数y=$\frac{k}{x}$(k≠0)在第一象限的图象经过顶点A(m,m+1)和CD边上的点E的纵坐标为$\frac{2}{3}$,过点E的直线l交于x轴于点F,交y轴于点G(0,-2),则OB:BF:FC为( )| A. | 5:4:3 | B. | 4:5:3 | C. | 1:1:1 | D. | 2:3:2 |
分析 先根据点A(m,m+1)可知正方形的边长为m+1,故E(2m+1,$\frac{2}{3}$),根据反比例函数图象上点的坐标特点求出m的值,故可得出E点坐标,利用待定系数法求出直线EG的解析式,进而可得出BF及CF的长,由此可得出结论.
解答 解:∵点A(m,m+1),
∴正方形的边长为m+1,
∴E(2m+1,$\frac{2}{3}$),
∴m(m+1)=$\frac{2}{3}$×(3m+1),解得m=1,
∴OB=1,E(3,$\frac{2}{3}$),
设直线EG的解析式为y=kx+b(k≠0),
∵点G(0,-2),
∴$\left\{\begin{array}{l}3k+b=\frac{2}{3}\\ b=-2\end{array}\right.$,解得$\left\{\begin{array}{l}k=\frac{8}{9}\\ b=-2\end{array}\right.$,
∴直线EG的解析式为y=$\frac{8}{9}$x-2,
∴F($\frac{9}{4}$,0),
∴BF=$\frac{5}{4}$,CF=$\frac{3}{4}$,
∴OB:BF:FC=1:$\frac{5}{4}$:$\frac{3}{4}$=4:5:3.
故选B.
点评 本题考查的是反比例函数综合题,熟知反比例函数图象上点的坐标特点是解答此题的关键.

练习册系列答案
 王后雄学案教材完全解读系列答案
王后雄学案教材完全解读系列答案
相关题目
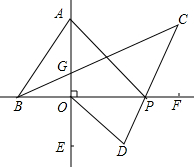 如图,直线AE⊥BF于O,将一个三角板ABO如图放置(∠BAO=30°),两直角边与直线BF,AE重合,P为直线BF上一动点,BC平分∠ABP,PC平分∠APF,OD平分∠POE.
如图,直线AE⊥BF于O,将一个三角板ABO如图放置(∠BAO=30°),两直角边与直线BF,AE重合,P为直线BF上一动点,BC平分∠ABP,PC平分∠APF,OD平分∠POE.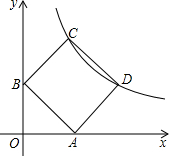 如图,在平面直角坐标系中,反比例函数y=$\frac{k}{x}$的图象两点C、D,以CD为边作正方形ABCD,点A、B分别在x轴、y轴的正半轴上,点B坐标为(0,1)且∠ABO=45°.
如图,在平面直角坐标系中,反比例函数y=$\frac{k}{x}$的图象两点C、D,以CD为边作正方形ABCD,点A、B分别在x轴、y轴的正半轴上,点B坐标为(0,1)且∠ABO=45°.