题目内容
甲乙两人在一长800米的环形跑道上练习长跑,甲的速度是120米/分,乙的速度是100米/分.
(1)若甲乙两人从相距140米的两地背向而行,问几分钟后两人相遇?
(2)若甲乙两人同时同地同向出发,问几分钟两人相遇?
(1)若甲乙两人从相距140米的两地背向而行,问几分钟后两人相遇?
(2)若甲乙两人同时同地同向出发,问几分钟两人相遇?
考点:一元一次方程的应用
专题:
分析:(1)根据两人长跑的过程中当第一次两人相遇时路程的和为(800-140)米,列出方程求解即可;
(2)根据两人长跑的过程中当第一次两人相遇时路程的差为800米,列出方程求解即可.
(2)根据两人长跑的过程中当第一次两人相遇时路程的差为800米,列出方程求解即可.
解答:解:(1)设x分钟后两人第一次相遇,
由题意得,120x+100x+140=800,
解得:x=3,
答:3分钟后两人第一次相遇;
(2)设甲乙两人同时同地同向出发,y分钟两人第一次相遇,
由题意得,120y-100y=800,
解得:y=40,
答:两人从同一地点同时同向起跑,40分钟后两人第一次相遇..
由题意得,120x+100x+140=800,
解得:x=3,
答:3分钟后两人第一次相遇;
(2)设甲乙两人同时同地同向出发,y分钟两人第一次相遇,
由题意得,120y-100y=800,
解得:y=40,
答:两人从同一地点同时同向起跑,40分钟后两人第一次相遇..
点评:本题考查了一元一次方程的应用,记住有关追击问题中的等量关系是解决本题的关键.

练习册系列答案
 小学生10分钟口算测试100分系列答案
小学生10分钟口算测试100分系列答案
相关题目
-(-
)的相反数是( )
| 1 |
| 2 |
A、
| ||
B、-
| ||
| C、2 | ||
| D、-2 |

 已知:如图,AB是⊙O的直径,点D在⊙O上,OC∥AD交⊙O于E,点F在CD延长线上,且∠BOC+∠ADF=90°.求证:CD是⊙O的切线.
已知:如图,AB是⊙O的直径,点D在⊙O上,OC∥AD交⊙O于E,点F在CD延长线上,且∠BOC+∠ADF=90°.求证:CD是⊙O的切线.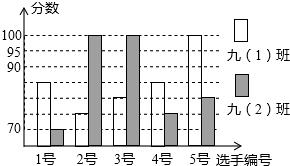 某中学开展“我的中国梦”演讲比赛活动,九(1)、九(2)班根据初赛成绩各选出5名选手参加复赛,两个班各选出的5名选手的复赛成绩(满分为100分)如下图所示.
某中学开展“我的中国梦”演讲比赛活动,九(1)、九(2)班根据初赛成绩各选出5名选手参加复赛,两个班各选出的5名选手的复赛成绩(满分为100分)如下图所示. 一条排水管的截面如图所示,已知水面宽AB=10cm,截面圆⊙O的半径OC⊥AB于D,且OD:DC=3:2,求⊙O的直径.
一条排水管的截面如图所示,已知水面宽AB=10cm,截面圆⊙O的半径OC⊥AB于D,且OD:DC=3:2,求⊙O的直径.