题目内容
3.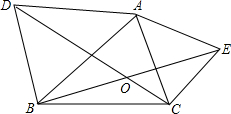 已知,如图,AB=AD,AC=AE,∠DAB=∠CAE=50°.
已知,如图,AB=AD,AC=AE,∠DAB=∠CAE=50°.(1)求证:△ABE≌△ADC.
(2)△ABE经过怎样的变换可以与△ADC重合?
(3)求∠BOD的度数.
分析 (1)根据SAS证明△ABE≌△ADC即可;
(2)根据旋转的性质得出△ABE与△ADC重合;
(3)根据全等三角形的性质和三角形的内角和解答即可.
解答 证明:(1)∵∠DAB=∠CAE=50°,
∴∠DAB+∠BAC=∠CAE+∠BAC,
∴∠DAC=∠BAE,
在△DAC与△BAE中,
$\left\{\begin{array}{l}{AD=AB}\\{∠DAC=∠BAE}\\{AC=AE}\end{array}\right.$,
∴△ABE≌△ADC(SAS);
(2)因为△ABE≌△ADC,∠DAB=∠CAE=50°,
可得:△ABE经过顺时针旋转50°可以与△ADC重合;
(3)如图:
∵△ABE≌△ADC,
∴∠ADC=∠ABE,
∵∠AFD=∠CFB,
∴∠BOD=∠DAB=50°.
点评 此题考查全等三角形的判定和性质,关键是根据SAS证明△ABE≌△ADC.

练习册系列答案
 尖子生新课堂课时作业系列答案
尖子生新课堂课时作业系列答案
相关题目
14. 小敏从A地出发向B地行走,同时小聪从B地出发向A地行走,如图所示,相交于点P的两条线段l1、l2分别表示小敏、小聪离B地的距离ykm与已用时间xh之间的关系,则小敏、小聪行走的速度分别是( )
小敏从A地出发向B地行走,同时小聪从B地出发向A地行走,如图所示,相交于点P的两条线段l1、l2分别表示小敏、小聪离B地的距离ykm与已用时间xh之间的关系,则小敏、小聪行走的速度分别是( )
 小敏从A地出发向B地行走,同时小聪从B地出发向A地行走,如图所示,相交于点P的两条线段l1、l2分别表示小敏、小聪离B地的距离ykm与已用时间xh之间的关系,则小敏、小聪行走的速度分别是( )
小敏从A地出发向B地行走,同时小聪从B地出发向A地行走,如图所示,相交于点P的两条线段l1、l2分别表示小敏、小聪离B地的距离ykm与已用时间xh之间的关系,则小敏、小聪行走的速度分别是( )| A. | 3km/h和4km/h | B. | 3km/h和3km/h | C. | 4km/h和4km/h | D. | 4km/h和3km/h |
11.下列四个式子中,结果为负数的是( )
| A. | (-1)2 | B. | (-1)×(-2) | C. | (-1)+(-2) | D. | (-1)-(-2) |
15.将抛物线y=x2+2向右平移3个单位后所得抛物线的解析式为( )
| A. | y=(x-3)2+2 | B. | y=x2+5 | C. | y=(x+3)2+2 | D. | y=x2-1 |
 如图:在△ABC中,BF=CF,BD⊥AC于D,CE⊥AB于E,BD、CE相交于F.
如图:在△ABC中,BF=CF,BD⊥AC于D,CE⊥AB于E,BD、CE相交于F.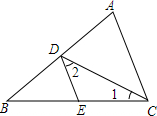 如图所示,CD是△ABC的角平分线,E是BC边上的一点,且∠1=∠2.试判断DE与AC的位置关系并说明理由.
如图所示,CD是△ABC的角平分线,E是BC边上的一点,且∠1=∠2.试判断DE与AC的位置关系并说明理由.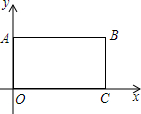 如图,在平面直角坐标系中,矩形OABC四个顶点的坐标分别为O(0,0),A(0,3),B(6,3),C(6,0),抛物线过y=ax2+bx+c(a≠0)点A.
如图,在平面直角坐标系中,矩形OABC四个顶点的坐标分别为O(0,0),A(0,3),B(6,3),C(6,0),抛物线过y=ax2+bx+c(a≠0)点A.