题目内容
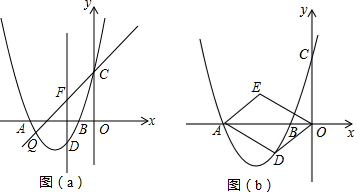
4. 如图,直线y1=$\frac{1}{2}$x+2与双曲线y2=$\frac{6}{x}$交于A(2,m)、B(-6,n)两点.则当y1<y2时,x的取值范围是( )
如图,直线y1=$\frac{1}{2}$x+2与双曲线y2=$\frac{6}{x}$交于A(2,m)、B(-6,n)两点.则当y1<y2时,x的取值范围是( )| A. | x>-6或0<x<2 | B. | -6<x<0或x>2 | C. | x<-6或0<x<2 | D. | -6<x<2 |
分析 (1)根据函数图象的上下关系,结合交点的横坐标找出不等式y1<y2的解集,由此即可得出结论.
解答 解:观察函数图象,发现:
当x<-6或0<x<2时,直线y1=$\frac{1}{2}$x+2的图象在双曲线y2=$\frac{6}{x}$的图象的下方,
∴当y1<y2时,x的取值范围是x<-6或0<x<2.
故选C.
点评 本题考查了反比例函数与一次函数的交点问题,解题的关键是依据函数图象的上下关系解不等式.本题属于基础题,难度不大,解决该题型题目时,根据函数图象位置的上下关系结合交点的坐标,找出不等式的解集是关键.

练习册系列答案
相关题目
15. 如图,直线l∥m,将含有45°角的三角板ABC的直角顶点C放在直线m上,若∠2=25°,则∠1的度数为( )
如图,直线l∥m,将含有45°角的三角板ABC的直角顶点C放在直线m上,若∠2=25°,则∠1的度数为( )
 如图,直线l∥m,将含有45°角的三角板ABC的直角顶点C放在直线m上,若∠2=25°,则∠1的度数为( )
如图,直线l∥m,将含有45°角的三角板ABC的直角顶点C放在直线m上,若∠2=25°,则∠1的度数为( )| A. | 20° | B. | 25° | C. | 30° | D. | 35° |
19.计算3-2的结果正确的是( )
| A. | $\frac{1}{9}$ | B. | -$\frac{1}{9}$ | C. | 9 | D. | -9 |
16.据统计,2015年长沙市的常住人口约为7500000人,将数据7500000用科学记数法表示为( )
| A. | 7.5×106 | B. | 0.75×107 | C. | 7.5×107 | D. | 75×105 |