题目内容
8.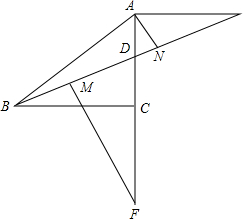 已知:如图,等腰Rt△ABC中,D为AC上一点,AE∥BC交BD延长线于E,AN⊥BE于N,在BE上截取MB=AN,过M作MF⊥BE交AC延长线于F,求证:CF=BC.
已知:如图,等腰Rt△ABC中,D为AC上一点,AE∥BC交BD延长线于E,AN⊥BE于N,在BE上截取MB=AN,过M作MF⊥BE交AC延长线于F,求证:CF=BC.
分析 首先证明∠3=∠2,然后可证明△BMH≌△AND,进而可得BH=AD,再由条件AC=BC,可得DC=HC,然后证明△DCB≌△HCF,根据全等三角形的性质可得CB=CF.
解答  证明:∵AE∥BC,
证明:∵AE∥BC,
∴∠E=∠3,∠EAD=∠ACB=90°,
∵AN⊥BE,
∴∠1+∠E=90°,∠ANE=90°,
∵∠BAC=90°,
∴∠1+∠2=90°,
∴∠2=∠E,
∴∠3=∠2,
在△BMH和△AND中,
$\left\{\begin{array}{l}{∠2=∠3}\\{AN=MB}\\{∠AND=∠BMH}\end{array}\right.$,
∴△BMH≌△AND(ASA),
∴BH=AD,
∵AC=BC,
∴DC=HC,
∵AN⊥EB,FM⊥EB,
∴MF∥AN,
∴∠2=∠F,
∴∠3=∠F,
在△DBC和△HCF中,
$\left\{\begin{array}{l}{∠3=∠F}\\{∠DCB=∠HCF}\\{DC=HC}\end{array}\right.$,
∴△DCB≌△HCF(AAS),
∴CB=CF.
点评 此题主要考查了全等三角形的判定与性质,关键是正确证明DC=HC,再证明出△DCB≌△HCF.

练习册系列答案
相关题目
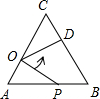 如图,在等边△ABC中,AC=9,点O在AC上,且AO=4,点P是AB上一动点,连结OP,将线段OP绕点O逆时针旋转60°得到线段OD.要使点D恰好落在BC上,则AP的长是5.
如图,在等边△ABC中,AC=9,点O在AC上,且AO=4,点P是AB上一动点,连结OP,将线段OP绕点O逆时针旋转60°得到线段OD.要使点D恰好落在BC上,则AP的长是5. 已知P为平行四边形ABCD的BC延长线上一点,AP交CD于Q,如果△DPQ的面积是100cm2,求△BCQ的面积.
已知P为平行四边形ABCD的BC延长线上一点,AP交CD于Q,如果△DPQ的面积是100cm2,求△BCQ的面积.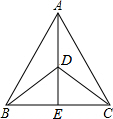 如图,在△ABC中,AB=AC,DB=DC,AD的延长线交BC于点E,求证:∠BAE=∠CAE.
如图,在△ABC中,AB=AC,DB=DC,AD的延长线交BC于点E,求证:∠BAE=∠CAE.