题目内容
18. 如图,已知三角形ABC的边AB是⊙0的切线,切点为B.AC经过圆心0并与圆相交于点D、C,过C作直线CE丄AB,交AB的延长线于点E.
如图,已知三角形ABC的边AB是⊙0的切线,切点为B.AC经过圆心0并与圆相交于点D、C,过C作直线CE丄AB,交AB的延长线于点E.(1)求证:CB平分∠ACE;
(2)若BE=3,CE=4,求⊙O的半径.
分析 (1)证明:如图1,连接OB,由AB是⊙0的切线,得到OB⊥AB,由于CE丄AB,的OB∥CE,于是得到∠1=∠3,根据等腰三角形的性质得到∠1=∠2,通过等量代换得到结果.
(2)如图2,连接BD通过△DBC∽△CBE,得到比例式$\frac{CD}{BC}=\frac{BC}{CE}$,列方程可得结果.
解答 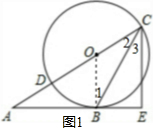 (1)证明:如图1,连接OB,
(1)证明:如图1,连接OB,
∵AB是⊙0的切线,
∴OB⊥AB,
∵CE丄AB,
∴OB∥CE,
∴∠1=∠3,
∵OB=OC,
∴∠1=∠2,
∴∠2=∠3,
∴CB平分∠ACE;
(2)如图2,连接BD,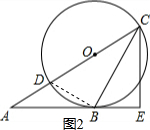
∵CE丄AB,
∴∠E=90°,
∴BC=$\sqrt{{BE}^{2}{+CE}^{2}}$=$\sqrt{{3}^{2}{+4}^{2}}$=5,
∵CD是⊙O的直径,
∴∠DBC=90°,
∴∠E=∠DBC,
∴△DBC∽△CBE,
∴$\frac{CD}{BC}=\frac{BC}{CE}$,
∴BC2=CD•CE,
∴CD=$\frac{{5}^{2}}{4}$=$\frac{25}{4}$,
∴OC=$\frac{1}{2}CD$=$\frac{25}{8}$,
∴⊙O的半径=$\frac{25}{8}$.
点评 本题考查了切线的性质,勾股定理,相似三角形的判定和性质,圆周角定理,平行线的判定和性质,正确的作出辅助线是解题的关键.

练习册系列答案
相关题目
8.若抛物线y=(x-m)2+(m+1)的顶点在第一象限,则m的取值范围为( )
| A. | m>1 | B. | m>0 | C. | m>-1 | D. | -1<m<0 |
9.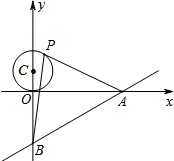 如图,已知直线y=$\frac{3}{4}$x-3与x轴、y轴分别交于A、B两点,P是以C(0,1)为圆心,1为半径的圆上一动点,连结PA、PB.则△PAB面积的最大值是( )
如图,已知直线y=$\frac{3}{4}$x-3与x轴、y轴分别交于A、B两点,P是以C(0,1)为圆心,1为半径的圆上一动点,连结PA、PB.则△PAB面积的最大值是( )
 如图,已知直线y=$\frac{3}{4}$x-3与x轴、y轴分别交于A、B两点,P是以C(0,1)为圆心,1为半径的圆上一动点,连结PA、PB.则△PAB面积的最大值是( )
如图,已知直线y=$\frac{3}{4}$x-3与x轴、y轴分别交于A、B两点,P是以C(0,1)为圆心,1为半径的圆上一动点,连结PA、PB.则△PAB面积的最大值是( )| A. | 8 | B. | 12 | C. | $\frac{21}{2}$ | D. | $\frac{17}{2}$ |

 如图是一个由4个相同的正方体组成的立体图形,它的主视图是( )
如图是一个由4个相同的正方体组成的立体图形,它的主视图是( )



 如图,在△ABC中,DE∥BC,分别交AB,AC于点D、E.若AD=3,DB=2,BC=6,则DE的长为3.6.
如图,在△ABC中,DE∥BC,分别交AB,AC于点D、E.若AD=3,DB=2,BC=6,则DE的长为3.6. 如图,四边形ABCD为矩形,过点D作对角线BD的垂线,交BC的延长线于点E,取BE的中点F,连接DF,DF=4.设AB=x,AD=y,则x2+(y-4)2的值为16.
如图,四边形ABCD为矩形,过点D作对角线BD的垂线,交BC的延长线于点E,取BE的中点F,连接DF,DF=4.设AB=x,AD=y,则x2+(y-4)2的值为16. 如图,已知直线a∥b,∠1=120°,则∠2的度数是60°.
如图,已知直线a∥b,∠1=120°,则∠2的度数是60°.