题目内容
已知实数a、b满足|a+2|+|1-a|=9-|b-5|-|1+b|,设a+b的最大值为m,最小值为n,则m+n的值为 .
考点:绝对值
专题:
分析:原式化为|a+2|+|a-1|+|b+1|+|b-5|=9,a分三种情况讨论:a≤-2,-2<a<1,a≥1;b也是分三种情况:b≤-1,-1<b<5,b≥5,分情况讨论,一共9种情况,最后得出a+b最大可取6,最小为-3,因此m+n=3.
解答:解:原式化为:|a+2|+|a-1|+|b+1|+|b-5|=9,
a分三种情况讨论:a≤-2,-2<a<1,a≥1
当a≤-2时,|a+2|+|a-1|=-2a-1;
当-2<a<1时,|a+2|+|a-1|=3;
当a≥1时,|a+2|+|a-1|=2a+1;
b也是分三种情况:b≤-1,-1<b<5,b≥5
|b+1|+|b-5|=-2b+4或 6 或2b-4,
分情况讨论,一共9种情况,
①当a≤-2,b≤-1时,-2a-1-2b+4=9,
∴a+b=-3;
②当a≤-2,-1<b<5时,-2a-1+6=9,
∴a=-2,
∴a+b最大值小于3,最小值大于-3;
③当a≤-2,b≥5时,-2a-1+2b-4=9,
∴a-b=-7,
∴a+b最大值为3;
④当-2<a<1,b≤-1时,3-2b+4=9,
∴b=-1,
∴a+b最大值小于0,最小值大于-3;
⑤当-2<a<1,-1<b<5时,3+6=9,
∴a+b最大值小于6,最小值大于-3;
⑥当-2<a<1,b≥5时,3+2b-4=9,
∴b=5,
∴a+b最大值为6,最小值大于3;
⑦当a≥1,b≤-1时,2a+1-2b+4=9,
∴a-b=2,
∴a+b最大值小于0,最小值大于-2;
⑧当a≥1,b≤-1时,2a+1+6=9,
∴a=
,
∴a+b最大值
,没有最小值;
⑨当a≥1,b≤-1时,2a+1+2b-4=9,
∴a+b=6;
最后得出a+b最大可取6,最小为-3,因此m+n=3.
故答案为:3.
a分三种情况讨论:a≤-2,-2<a<1,a≥1
当a≤-2时,|a+2|+|a-1|=-2a-1;
当-2<a<1时,|a+2|+|a-1|=3;
当a≥1时,|a+2|+|a-1|=2a+1;
b也是分三种情况:b≤-1,-1<b<5,b≥5
|b+1|+|b-5|=-2b+4或 6 或2b-4,
分情况讨论,一共9种情况,
①当a≤-2,b≤-1时,-2a-1-2b+4=9,
∴a+b=-3;
②当a≤-2,-1<b<5时,-2a-1+6=9,
∴a=-2,
∴a+b最大值小于3,最小值大于-3;
③当a≤-2,b≥5时,-2a-1+2b-4=9,
∴a-b=-7,
∴a+b最大值为3;
④当-2<a<1,b≤-1时,3-2b+4=9,
∴b=-1,
∴a+b最大值小于0,最小值大于-3;
⑤当-2<a<1,-1<b<5时,3+6=9,
∴a+b最大值小于6,最小值大于-3;
⑥当-2<a<1,b≥5时,3+2b-4=9,
∴b=5,
∴a+b最大值为6,最小值大于3;
⑦当a≥1,b≤-1时,2a+1-2b+4=9,
∴a-b=2,
∴a+b最大值小于0,最小值大于-2;
⑧当a≥1,b≤-1时,2a+1+6=9,
∴a=
| 3 |
| 2 |
∴a+b最大值
| 1 |
| 2 |
⑨当a≥1,b≤-1时,2a+1+2b-4=9,
∴a+b=6;
最后得出a+b最大可取6,最小为-3,因此m+n=3.
故答案为:3.
点评:本题主要考查了绝对值的知识点,解答本题的关键是分类讨论得出a+b的最大值和最小值.

练习册系列答案
 天天向上课时同步训练系列答案
天天向上课时同步训练系列答案 阳光课堂同步练习系列答案
阳光课堂同步练习系列答案
相关题目
 如图,AB∥CD,∠E=27°,∠B=52°,则∠ECD为( )度.
如图,AB∥CD,∠E=27°,∠B=52°,则∠ECD为( )度.| A、63 | B、79 | C、101 | D、25 |
云南省2013年教育经费投入超过900亿元,900亿用科学记数法表示为( )
| A、900×108 |
| B、9×1010 |
| C、9×1011 |
| D、0.9×1011 |
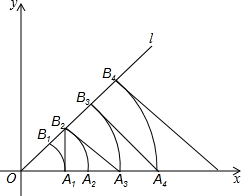 如图,已知直线l的表达式为y=x,点A1的坐标为(1,0),以O为圆心,OA1为半径画弧,与直线l交于点B1,过点A1作x轴的垂线交直线l于点B2,以O为圆心,OB2为半径画弧,交x轴于A2;过点B2作直线l的垂线交x轴于点A3,以O为圆心,OA3为半径画弧,交直线l于B3;过点B3作直线,的垂线交x轴于点A4,以O为圆心,OA4为半径画弧,交直线l于B4,过点B4作直线l的垂线交x轴于点A5…按照这样规律进行下去,点B2014的坐标为
如图,已知直线l的表达式为y=x,点A1的坐标为(1,0),以O为圆心,OA1为半径画弧,与直线l交于点B1,过点A1作x轴的垂线交直线l于点B2,以O为圆心,OB2为半径画弧,交x轴于A2;过点B2作直线l的垂线交x轴于点A3,以O为圆心,OA3为半径画弧,交直线l于B3;过点B3作直线,的垂线交x轴于点A4,以O为圆心,OA4为半径画弧,交直线l于B4,过点B4作直线l的垂线交x轴于点A5…按照这样规律进行下去,点B2014的坐标为 如图,填空:
如图,填空: