题目内容
有一个一元二次方程,它的一个根x1=-1,另一个根x2=2.8,请你写出一个符合这样条件的方程: .
考点:根与系数的关系
专题:开放型
分析:根据所给两根的值,易求x1+x2=1.8,x1x2=-2.8,可令a=1,进而可求b、c的值.
解答:解:∵x1=-1,x2=2.8,
∴x1+x2=1.8,x1x2=-2.8,
若令a=1,则b=-1.8,c=-2.8,
故所求方程是x2-1.8x-2.8=0(答案不唯一),
故答案为:x2-1.8x-2.8=0(答案不唯一).
∴x1+x2=1.8,x1x2=-2.8,
若令a=1,则b=-1.8,c=-2.8,
故所求方程是x2-1.8x-2.8=0(答案不唯一),
故答案为:x2-1.8x-2.8=0(答案不唯一).
点评:本题考查了根与系数的关系,解题的关键是能根据两个根求出相应的方程,注意方程不唯一.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
 如图,AB∥EF,BC∥DE,则∠B与∠E的关系是
如图,AB∥EF,BC∥DE,则∠B与∠E的关系是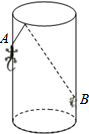 如图,圆柱形容器中,高为1.2米,底面周长为1米,在容器内壁离容器底部0.3m处的点B处有一蚊子.此时,一只壁虎正好在容器外壁,离容器上沿0.3m与蚊子相对的点A处,则壁虎捕捉蚊子的最短距离为( )米.
如图,圆柱形容器中,高为1.2米,底面周长为1米,在容器内壁离容器底部0.3m处的点B处有一蚊子.此时,一只壁虎正好在容器外壁,离容器上沿0.3m与蚊子相对的点A处,则壁虎捕捉蚊子的最短距离为( )米.