题目内容
9.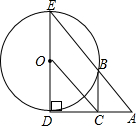 如图.己知DE是⊙O的直径,过点D作⊙O的切线AD,C是AD的中点,AE交⊙O于B点,连接BC.
如图.己知DE是⊙O的直径,过点D作⊙O的切线AD,C是AD的中点,AE交⊙O于B点,连接BC.(1)BC是⊙O的切线吗?若是,给出证明:若不是,说明理由.
(2)四边形BCOE是平行四边形吗?若是,给出证明;若不是,说明理由.
分析 (1)连接OB,由BC与OD平行,BC=OD,得到四边形BCDO为平行四边形,由AD为圆的切线,利用切线的性质得到OD垂直于AD,可得出四边形BCDO为矩形,利用矩形的性质得到OB垂直于BC,即可得出BC为圆O的切线;
(2)四边形BCOE不一定是平行四边形,根据已知条件只能证出一组对边平行,于是得到结论.
解答 解:(1)是,理由如下:
如图,连接OB,BD,
∵DE是⊙O的直径,
∴BD⊥AE,
∵C是AD的中点,
∴BC=CD,
在△CDO与△CBO中,
$\left\{\begin{array}{l}{OD=OB}\\{BC=DC}\\{OC=OC}\end{array}\right.$,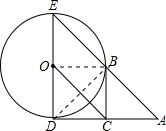
∴△COD≌△COB,
∴∠OBC=∠ODC,
∵AD是⊙O的切线,
∴∠CDO=90°,
∴∠CBO=90°,
∴OB⊥BC,
则BC为圆O的切线;
(2)四边形BCOE不一定是平行四边形,
理由:∵DO=EO,DC=AC,
∴OC∥AE,
根据已知条件证不出BC∥DE或OC=BE,
∴四边形BCOE为平行四边形.
点评 此题考查了切线的判定与性质,直角三角形斜边上的中线性质,以及平行四边形的判定与性质,熟练掌握切线的判定与性质是解本题的关键.

练习册系列答案
相关题目
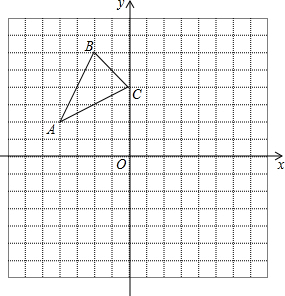 如图,已知A(-4,2),B(-2,6),C(0,4)是直角坐标系平面上三点.
如图,已知A(-4,2),B(-2,6),C(0,4)是直角坐标系平面上三点.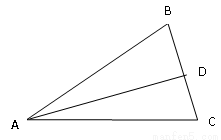
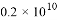 B.
B. 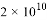 C.
C. 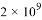 D.
D. 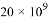
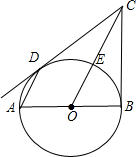 如图,BC切⊙O于点B,AB为⊙O的直径,弦AD∥OC,OC交⊙O于点E.求证:
如图,BC切⊙O于点B,AB为⊙O的直径,弦AD∥OC,OC交⊙O于点E.求证: 如图,△ABC中,AB=AC,以AB为直径的⊙O交BC于D,过D作⊙O的切线交AC于E
如图,△ABC中,AB=AC,以AB为直径的⊙O交BC于D,过D作⊙O的切线交AC于E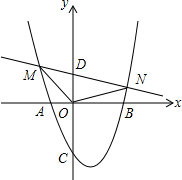 已知,抛物线y=ax2-(a+m-2)x-a-2m+4与x轴交于A(-1,0),B(x,0)两点,与y轴负半轴交于点C,且OA+OB=OC+1.
已知,抛物线y=ax2-(a+m-2)x-a-2m+4与x轴交于A(-1,0),B(x,0)两点,与y轴负半轴交于点C,且OA+OB=OC+1.