题目内容
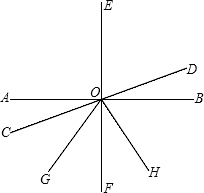 如图,AB、CD、EF相交于点O,EF⊥AB,OG、OH分别为∠COF、∠DOG的平分线,若∠AOC:∠COG=4:7,则∠DOF=
如图,AB、CD、EF相交于点O,EF⊥AB,OG、OH分别为∠COF、∠DOG的平分线,若∠AOC:∠COG=4:7,则∠DOF=考点:垂线,对顶角、邻补角
专题:
分析:利用垂直定义结合已知设∠AOC=4x,∠COG=7x,则∠GOF=7x,进而求出x的值,再利用角平分线的性质得出答案.
解答:解:∵EF⊥AB,OG为∠COF的平分线,
∴∠COG=∠FOG,
∵∠AOC:∠COG=4:7,
∴设∠AOC=4x,∠COG=7x,则∠GOF=7x,
∴4x+7x+7x=18x=90°,
解得:x=5°,
故∠AOC=∠DOB=20°,∠COG=∠GOF=35°,
则∠DOF=90°+20°=110°,
故∠DOG=20°+90°+35°=145°,
故∠GOH=∠DOH=72.5°,
故答案为:110°,72.5°.
∴∠COG=∠FOG,
∵∠AOC:∠COG=4:7,
∴设∠AOC=4x,∠COG=7x,则∠GOF=7x,
∴4x+7x+7x=18x=90°,
解得:x=5°,
故∠AOC=∠DOB=20°,∠COG=∠GOF=35°,
则∠DOF=90°+20°=110°,
故∠DOG=20°+90°+35°=145°,
故∠GOH=∠DOH=72.5°,
故答案为:110°,72.5°.
点评:此题主要考查了角平分线的定义以及垂线的定义,熟练应用角平分线的定义是解题关键.

练习册系列答案
 浙大优学小学年级衔接导与练浙江大学出版社系列答案
浙大优学小学年级衔接导与练浙江大学出版社系列答案 小学暑假作业东南大学出版社系列答案
小学暑假作业东南大学出版社系列答案 津桥教育暑假拔高衔接广东人民出版社系列答案
津桥教育暑假拔高衔接广东人民出版社系列答案 波波熊暑假作业江西人民出版社系列答案
波波熊暑假作业江西人民出版社系列答案
相关题目
 如图,在一个4×4的正方形网格中,现将其中的两个小正方形涂上阴影,请你用两种不同的方法分别在图中再将两个空白的小正方形涂上阴影,使它关于某点成中心对称,并用字母标出对称中心.
如图,在一个4×4的正方形网格中,现将其中的两个小正方形涂上阴影,请你用两种不同的方法分别在图中再将两个空白的小正方形涂上阴影,使它关于某点成中心对称,并用字母标出对称中心. 如图,在△ABC中,点D在边BC上,连接AD,BC=BD+AD.点D在哪条线段的垂直平分线上?证明你的结论.
如图,在△ABC中,点D在边BC上,连接AD,BC=BD+AD.点D在哪条线段的垂直平分线上?证明你的结论. 如图,已知矩形ABCD的对角线AC与BD相交于点O,OF⊥AD于点F,OF=3cm,AE⊥BD于点E,且BE:ED=1:3,求AC的长.
如图,已知矩形ABCD的对角线AC与BD相交于点O,OF⊥AD于点F,OF=3cm,AE⊥BD于点E,且BE:ED=1:3,求AC的长.