题目内容
4.先化简再求值:$\frac{1}{2}$x-2(x-$\frac{1}{3}$y2)+(-$\frac{3}{2}$x+$\frac{1}{3}$y2),其中x=1,y=$\frac{1}{2}$.分析 原式去括号合并得到最简结果,把x与y的值代入计算即可求出值.
解答 解:原式=$\frac{1}{2}$x-2x+$\frac{2}{3}$y2-$\frac{3}{2}$x+$\frac{1}{3}$y2=-3x+y2,
当x=1,y=$\frac{1}{2}$时,原式=-3×1+($\frac{1}{2}$)2=-3+$\frac{1}{4}$=-2$\frac{3}{4}$.
点评 此题考查了整式的加减-化简求值,熟练掌握运算法则是解本题的关键.

练习册系列答案
 快乐暑假暑假能力自测中西书局系列答案
快乐暑假暑假能力自测中西书局系列答案
相关题目
14.某工艺厂计划一周生产工艺品1400个,平均每天生产200个,但实际每天生产量与计划相比有出入.表是某舟的生产情况(超产记为正、减产记为负):
(1)写出该厂星期三生产工艺品的数量;
(2)本周产量中最多的一天比最少的一天多生产多少个工艺品?
(3)请求出该工艺厂在本周实际生产工艺品的数量;
(4)已知该厂实行每周计件工资制,每生产一个工艺品可得30元,若超额完成任务;则超过部分每个另奖20元,少生产一个扣50元.试求该工艺厂在这一周应付出的工资总额.
| 星期 | 一 | 二 | 三 | 四 | 五 | 六 | 日 |
| 增减(单位:个) | +5 | -2 | -5 | +15 | -10 | +12 | -9 |
(2)本周产量中最多的一天比最少的一天多生产多少个工艺品?
(3)请求出该工艺厂在本周实际生产工艺品的数量;
(4)已知该厂实行每周计件工资制,每生产一个工艺品可得30元,若超额完成任务;则超过部分每个另奖20元,少生产一个扣50元.试求该工艺厂在这一周应付出的工资总额.
14.抛物线y=3x2,y=-3x2,y=-3x2+3共有的性质是( )
| A. | 开口向上 | B. | 对称轴是y轴 | ||
| C. | 都有最高点 | D. | y随x值的增大而增大 |
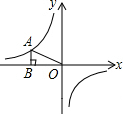 如图,过反比例函数y=$\frac{k}{x}$的图象上一点A作AB⊥x轴于点B,连接AO,若S△AOB=3,则k的值为-6.
如图,过反比例函数y=$\frac{k}{x}$的图象上一点A作AB⊥x轴于点B,连接AO,若S△AOB=3,则k的值为-6. 如图,△ABC绕点C旋转后,顶点A旋转到了点A′,用尺规画出旋转后的三角形并指出一个旋转角.
如图,△ABC绕点C旋转后,顶点A旋转到了点A′,用尺规画出旋转后的三角形并指出一个旋转角.